
ЁОЬтФПЁПЖЈвхЃКДгЪ§Са{an}жаГщШЁmЃЈmЁЪNЃЌmЁн3ЃЉЯюАДЦфдк{an}жаЕФДЮађХХСааЮГЩвЛИіаТЪ§Са{bn}ЃЌдђГЦ{bn}ЮЊ{an}ЕФзгЪ§СаЃЛШє{bn}ГЩЕШВюЃЈЛђЕШБШЃЉЃЌдђГЦ{bn}ЮЊ{an}ЕФЕШВюЃЈЛђЕШБШЃЉзгЪ§СаЃЎ
ЃЈ1ЃЉМЧЪ§Са{an}ЕФЧАnЯюКЭЮЊSnЃЌвбжЊ![]() ЃЎ
ЃЎ
ЂйЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЂкЪ§Са{an}ЪЧЗёДцдкЕШВюзгЪ§СаЃЌШєДцдкЃЌЧѓГіЕШВюзгЪ§СаЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉвбжЊЪ§Са{an}ЕФЭЈЯюЙЋЪНЮЊanЃНn+aЃЈaЁЪQ+ЃЉЃЌжЄУїЃК{an}ДцдкЕШБШзгЪ§СаЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЎЂкВЛДцдкЕШВюзгЪ§СаЃЎМћНтЮіЃЈ2ЃЉМћНтЮі
ЃЎЂкВЛДцдкЕШВюзгЪ§СаЃЎМћНтЮіЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОн![]() ЃЌЕБnЃН1ЪБЃЌ
ЃЌЕБnЃН1ЪБЃЌ![]() ЃЌЕБnЁн2ЪБЃЌЕУЕН
ЃЌЕБnЁн2ЪБЃЌЕУЕН![]() ЃЌСНЪНЯрМѕМДПЩ.ЂкМйЩшДгЪ§Са{an}жаГщ3ЯюakЃЌalЃЌamЃЈkЃМlЃМmЃЉГЩЕШВюЃЌРћгУЕШВюжаЯюдђ2alЃНak+amЃЌМД2ЁС2lЉ1ЃН2kЉ1+2mЉ1ЃЌ
ЃЌСНЪНЯрМѕМДПЩ.ЂкМйЩшДгЪ§Са{an}жаГщ3ЯюakЃЌalЃЌamЃЈkЃМlЃМmЃЉГЩЕШВюЃЌРћгУЕШВюжаЯюдђ2alЃНak+amЃЌМД2ЁС2lЉ1ЃН2kЉ1+2mЉ1ЃЌ
ЛЏМђЕУЃК2ЁС2lЉkЃН1+2mЉkЃЎдйРћгУЦцХМЪ§ХаЖЯ.ШчЙћДгЪ§Са{an}жаГщmЃЈmЁЪNЃЌmЁн4ЃЉЯюЃЌЦфЧАШ§ЯюБиГЩЕШВюЪ§СаЃЌВЛГЩСЂЕУжЄ.
ЃЈ2ЃЉМйЩшЪ§Са{an}жаДцдк3Яюn0+aЃЌn0+a+kЃЌn0+a+lЃЈkЃМlЃЉГЩЕШБШЃЎЩшn0+aЃНbЃЌдђbЁЪQ+ЃЌЙЪПЩЩш![]() ЃЈpгыqЪЧЛЅжЪЕФе§ећЪ§ЃЉЃЎИљОнЕШБШжаЯюЃЌга
ЃЈpгыqЪЧЛЅжЪЕФе§ећЪ§ЃЉЃЎИљОнЕШБШжаЯюЃЌга![]() ЃЌМД
ЃЌМД![]() ЃЎШЁkЃНqЃЌдђlЃН2k+pqЃЎдйТлжЄЃЈb+kЃЉ2=bЃЈb+lЃЉЪЧЗёГЩСЂМДПЩ.
ЃЎШЁkЃНqЃЌдђlЃН2k+pqЃЎдйТлжЄЃЈb+kЃЉ2=bЃЈb+lЃЉЪЧЗёГЩСЂМДПЩ.
ЃЈ1ЃЉЂйвђЮЊ![]() ЃЌЫљвдЕБnЃН1ЪБЃЌ
ЃЌЫљвдЕБnЃН1ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБnЁн2ЪБЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЎ
ЃЎ
злЩЯПЩжЊЃК![]() ЃЎ
ЃЎ
ЂкМйЩшДгЪ§Са{an}жаГщ3ЯюakЃЌalЃЌamЃЈkЃМlЃМmЃЉГЩЕШВюЃЌ
дђ2alЃНak+amЃЌМД2ЁС2lЉ1ЃН2kЉ1+2mЉ1ЃЌ
ЛЏМђЕУЃК2ЁС2lЉkЃН1+2mЉkЃЎ
вђЮЊkЃМlЃМmЃЌЫљвдlЉkЃО0ЃЌmЉkЃО0ЃЌЧвlЉkЃЌmЉkЖМЪЧећЪ§ЃЌ
Ыљвд2ЁС2lЉkЮЊХМЪ§ЃЌ1+2mЉkЮЊЦцЪ§ЃЌЫљвд2ЁС2lЉkЃН1+2mЉkВЛГЩСЂЃЎ
вђДЫЃЌЪ§Са{an}ВЛДцдкШ§ЯюЕШВюзгЪ§СаЃЎ
ШєДгЪ§Са{an}жаГщmЃЈmЁЪNЃЌmЁн4ЃЉЯюЃЌЦфЧАШ§ЯюБиГЩЕШВюЪ§СаЃЌВЛГЩСЂЃЎ
злЩЯПЩжЊЃЌЪ§Са{an}ВЛДцдкЕШВюзгЪ§СаЃЎ
ЃЈ2ЃЉМйЩшЪ§Са{an}жаДцдк3Яюn0+aЃЌn0+a+kЃЌn0+a+lЃЈkЃМlЃЉГЩЕШБШЃЎ
Щшn0+aЃНbЃЌдђbЁЪQ+ЃЌЙЪПЩЩш![]() ЃЈpгыqЪЧЛЅжЪЕФе§ећЪ§ЃЉЃЎ
ЃЈpгыqЪЧЛЅжЪЕФе§ећЪ§ЃЉЃЎ
дђашТњзу![]() ЃЌ
ЃЌ
МДашТњзуЃЈb+kЃЉ2ЃНbЃЈb+lЃЉЃЌдђашТњзу![]() ЃЎ
ЃЎ
ШЁkЃНqЃЌдђlЃН2k+pqЃЎ
ДЫЪБ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЙЪДЫЪБЃЈb+kЃЉ2ЃНbЃЈb+lЃЉГЩСЂЃЎ
вђДЫЪ§Са{an}жаДцдк3Яюn0+aЃЌn0+a+kЃЌn0+a+lЃЈkЃМlЃЉГЩЕШБШЃЌ
ЫљвдЪ§Са{an}ДцдкЕШБШзгЪ§СаЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЖрУцЬх![]() жаЃЌЫФБпаЮ
жаЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕу.
ЕФжаЕу.
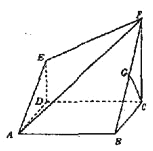
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЦНУц![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЕїНкИпШ§бЇЩњбЇЯАбЙСІЃЌФГаЃИпШ§ФъМЖОйааСЫАЮКгБШШќЃЌдкШќЧАШ§ЮЛРЯЪІЖдЧАШ§УћНјааСЫдЄВтЃЌгкЪЧгаСЫвдЯТЖдЛАЃКРЯЪІМзЃКЁА7АрФаЩњБШНЯзГЃЌ7АрПЯЖЈЕУЕквЛУћЁБЃЎРЯЪІввЃКЁАЮвОѕЕУ14АрБШ15АрЧПЃЌ14АрУћДЮЛсБШ15АрППЧАЁБЃЎРЯЪІБћЃКЁАЮвОѕЕУ7АрФмгЎ15АрЁБЃЎзюКѓРЯЪІЖЁШЅЙлПДЭъСЫБШШќЃЌЛиРДКѓЫЕЃКЁАШЗЪЕЪЧетШ§ИіАрЕУСЫЧАШ§УћЃЌЧвЮоВЂСаЃЌЕЋЪЧФуУЧШ§ШЫжажЛгавЛШЫдЄВтзМШЗЁБЃЎФЧУДЃЌЛёЕУвЛЁЂЖўЁЂШ§УћЕФАрМЖвРДЮЮЊ( )
A.7АрЁЂ14АрЁЂ15АрB.14АрЁЂ7АрЁЂ15Ар
C.14АрЁЂ15АрЁЂ7АрD.15АрЁЂ14АрЁЂ7Ар
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЙХДњЪ§бЇУћжјЁЖЫуЗЈЭГзкЁЗжагаШчЯТЮЪЬтЃКЁАдЖЭћЮЁЮЁЫўЦпВуЃЌКьЙтЕуЕуБЖМгдіЃЌЙВЕЦШ§АйАЫЪЎвЛЃЌЧыЮЪМтЭЗМИеЕЕЦЃПЁБвтЫМЪЧЃКвЛзљ7ВуЫўЙВЙвСЫ381еЕЕЦЃЌЧвЯрСкСНВужаЕФЯТвЛВуЕЦЪ§ЪЧЩЯвЛВуЕЦЪ§ЕФ2БЖЃЌдђЫўЕФЖЅВуЙВгаЕЦЃЈ ЃЉ
A. 1еЕ B. 3еЕ C. 5еЕ D. 9еЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнЁЖШЫУёЭјЁЗБЈЕРЃЌУРЙњЙњМвКНПеКНЬьОжЃЈNASAЃЉЗЂЮФГЦЃЌЯрБШ20ФъЧАЪРНчБфЕУИќТЬЩЋСЫЃЌЮРаЧзЪСЯЯдЪОжаЙњКЭгЁЖШЕФааЖЏжїЕМСЫЕиЧђБфТЬ.ОнЭГМЦЃЌжаЙњаТдіТЬЛЏУцЛ§ЕФ![]() РДздгкжВЪїдьСжЃЌЯТБэЪЧжаЙњЪЎИіЕиЧјдкШЅФъжВЪїдьСжЕФЯрЙиЪ§Он.ЃЈдьСжзмУцЛ§ЮЊШЫЙЄдьСжЁЂЗЩВЅдьСжЁЂаТЗтЩНг§СжЁЂЭЫЛЏСжаоИДЁЂШЫЙЄИќаТЕФУцЛ§жЎКЭЃЉ
РДздгкжВЪїдьСжЃЌЯТБэЪЧжаЙњЪЎИіЕиЧјдкШЅФъжВЪїдьСжЕФЯрЙиЪ§Он.ЃЈдьСжзмУцЛ§ЮЊШЫЙЄдьСжЁЂЗЩВЅдьСжЁЂаТЗтЩНг§СжЁЂЭЫЛЏСжаоИДЁЂШЫЙЄИќаТЕФУцЛ§жЎКЭЃЉ
ЕЅЮЛЃКЙЋЧъ
ЕиЧј | дьСжзмУцЛ§ | дьСжЗНЪН | ||||
ШЫЙЄдьСж | ЗЩВЅдьСж | аТЗтЩНг§Сж | ЭЫЛЏСжаоИД | ШЫЙЄИќаТ | ||
ФкУЩ | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
КгББ | 583361 | 345625 | 33333 | 13507 | 65653 | 3643 |
КгФЯ | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
жиЧь | 226333 | 100600 | 62400 | 63333 | ||
ЩТЮї | 297642 | 184108 | 33602 | 63865 | 16067 | |
ИЪЫр | 325580 | 260144 | 57438 | 7998 | ||
аТНЎ | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
ЧрКЃ | 178414 | 16051 | 159734 | 2629 | ||
ФўЯФ | 91531 | 58960 | 22938 | 8298 | 1335 | |
ББОЉ | 19064 | 10012 | 4000 | 3999 | 1053 | |
ЃЈ1ЃЉЧыИљОнЩЯЪіЪ§ОнЗжБ№аДГідкетЪЎИіЕиЧјжаШЫЙЄдьСжУцЛ§гыдьСжзмУцЛ§ЕФБШжЕзюДѓКЭзюаЁЕФЕиЧјЃЛ
ЃЈ2ЃЉдкетЪЎИіЕиЧјжаЃЌШЮбЁвЛИіЕиЧјЃЌЧѓИУЕиЧјаТЗтЩНг§СжУцЛ§еМдьСжзмУцЛ§ЕФБШжЕГЌЙ§![]() ЕФИХТЪЃЛ
ЕФИХТЪЃЛ
ЃЈ3ЃЉдкетЪЎИіЕиЧјжаЃЌДгЭЫЛЏСжаоИДУцЛ§ГЌЙ§вЛЭђЙЋЧъЕФЕиЧјжаЃЌШЮбЁСНИіЕиЧјЃЌМЧXЮЊетСНИіЕиЧјжаЭЫЛЏСжаоИДУцЛ§ГЌЙ§СљЭђЙЋЧъЕФЕиЧјЕФИіЪ§ЃЌЧѓXЕФЗжВМСаМАЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈtЮЊВЮЪ§ЃЌІСЁЪ[0ЃЌІаЃЉЃЎвдOЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊІбЃНІбcosІШ+2ЃЌ
ЃЈtЮЊВЮЪ§ЃЌІСЁЪ[0ЃЌІаЃЉЃЎвдOЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯпCЕФМЋзјБъЗНГЬЮЊІбЃНІбcosІШ+2ЃЌ
ЃЈ1ЃЉШє![]() ЃЌЧѓжБЯпЕФМЋзјБъЗНГЬ
ЃЌЧѓжБЯпЕФМЋзјБъЗНГЬ
ЃЈ2ЃЉШєжБЯпгыЧњЯпCгаЮЈвЛЙЋЙВЕуЃЌЧѓІС
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкСНИіЖЈвхгђОљЮЊDЕФКЏЪ§fЃЈxЃЉЃЌgЃЈxЃЉЃЌШєДцдкзюаЁе§ЪЕЪ§MЃЌЪЙЕУЖдгкШЮвтxЁЪDЃЌЖМга|fЃЈxЃЉЃgЃЈxЃЉ|ЁмMЃЌдђГЦMЮЊКЏЪ§fЃЈxЃЉЃЌgЃЈxЃЉЕФЁАВюОрЁБЃЌВЂМЧзї||fЃЈxЃЉЃЌgЃЈxЃЉ||ЃЎ
ЃЈ1ЃЉЧѓfЃЈxЃЉЃНsinxЃЈxЁЪRЃЉЃЌgЃЈxЃЉЃНcosxЃЈxЁЪRЃЉЕФВюОрЃЛ
ЃЈ2ЃЉЩшfЃЈxЃЉЃН![]() ЃЈxЁЪ[1,
ЃЈxЁЪ[1,![]() ]ЃЉЃЌgЃЈxЃЉЃНmlnx ЃЈxЁЪ[1,
]ЃЉЃЌgЃЈxЃЉЃНmlnx ЃЈxЁЪ[1,![]() ]ЃЉЃЎЃЈeЁж2.718ЃЉ
]ЃЉЃЎЃЈeЁж2.718ЃЉ
ЂйШєmЃН2ЃЌЧв||fЃЈxЃЉЃЌgЃЈxЃЉ||ЃН1ЃЌЧѓТњзуЬѕМўЕФзюДѓе§ећЪ§aЃЛ
ЂкШєaЃН2ЃЌЧв||fЃЈxЃЉЃЌgЃЈxЃЉ||ЃН2ЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЧњЯпCЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯпlЕФМЋзјБъЗНГЬЮЊ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯпlЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯпCЕФМЋзјБъЗНГЬКЭжБЯпlЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєЩфЯп![]() гыЧњЯпCНЛгкЕуAЃЈВЛЭЌгкМЋЕуOЃЉЃЌгыжБЯпlНЛгкЕуBЃЌЧѓ
гыЧњЯпCНЛгкЕуAЃЈВЛЭЌгкМЋЕуOЃЉЃЌгыжБЯпlНЛгкЕуBЃЌЧѓ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈxЃО0ЃЉЃЎ
ЃЈxЃО0ЃЉЃЎ
ЃЈ1ЃЉШєaЃН1ЃЌf(x)дкЃЈ0ЃЌЃЋЁоЃЉЩЯЪЧЕЅЕїдіКЏЪ§ЃЌЧѓbЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєaЁн2ЃЌbЃН1ЃЌЧѓЗНГЬ![]() дкЃЈ0ЃЌ1]ЩЯНтЕФИіЪ§ЃЎ
дкЃЈ0ЃЌ1]ЩЯНтЕФИіЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com