
 :
: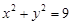 ,点
,点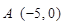 ,直线
,直线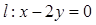 .
.
 相切,且与直线
相切,且与直线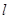 垂直的直线方程;
垂直的直线方程; 上(
上(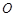 为坐标原点),存在定点
为坐标原点),存在定点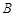 (不同于点
(不同于点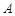 ),满足:对于圆
),满足:对于圆 上的任一点
上的任一点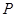 ,都有
,都有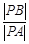 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点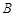 的坐标.
的坐标. (2)见解析
(2)见解析 (其中
(其中 表示圆心到直线的距离),可得到直线方程;
表示圆心到直线的距离),可得到直线方程;  ,由于
,由于 的位置不定,所以首先考虑特殊位置,①
的位置不定,所以首先考虑特殊位置,① 为圆
为圆 与
与 轴左交点或②
轴左交点或② 为圆
为圆 与
与 轴右交点这两种情况,由于对于圆
轴右交点这两种情况,由于对于圆 上的任一点
上的任一点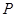 ,都有
,都有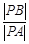 为一常数,所以①②两种情况下的
为一常数,所以①②两种情况下的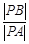 相等, 可得到
相等, 可得到 ,然后证明在一般的
,然后证明在一般的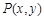 下,
下, 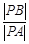 为一常数.
为一常数.  ,根据对于圆
,根据对于圆 上的任一点
上的任一点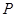 ,都有
,都有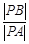 为一常数,设出
为一常数,设出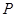 以及该常数
以及该常数 ,通过
,通过 ,代入
,代入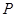 的坐标化简,转化为恒成立问题求解.
的坐标化简,转化为恒成立问题求解. ,因为所求直线与已知直线垂直,
,因为所求直线与已知直线垂直, ,即
,即 .
. ,其中
,其中 表示圆心到直线的距离,
表示圆心到直线的距离, ,得
,得 ,故所求直线方程为
,故所求直线方程为 .
.  ,
, 为圆
为圆 与
与 轴左交点
轴左交点 时,
时,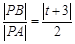 ,
, 为圆
为圆 与
与 轴右交点
轴右交点 时,
时,
 ,解得
,解得 (舍去),或
(舍去),或 .
. 对于圆
对于圆 上任一点
上任一点 ,都有
,都有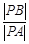 为一常数.
为一常数.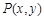 ,则
,则 .
. ,
, 为常数.
为常数.  ,使得
,使得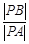 为常数
为常数 ,则
,则 ,
,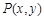 于是
于是 ,由于
,由于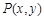 在圆上,所以
在圆上,所以 ,代入得,
,代入得,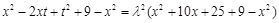 ,
, 对
对 恒成立,
恒成立,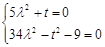 ,解得
,解得 或
或 (舍去),
(舍去), 对于圆
对于圆 上任一点
上任一点 ,都有
,都有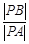 为一常数
为一常数 .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
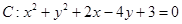 .
.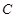 的切线在
的切线在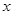 轴和
轴和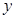 轴上的截距相等,且截距不为零,求此切线的方程;
轴上的截距相等,且截距不为零,求此切线的方程;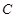 外一点
外一点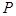 向该圆引一条切线,切点为
向该圆引一条切线,切点为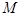 ,
,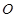 为坐标原点,且有
为坐标原点,且有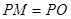 ,求使
,求使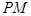 的长取得最小值的点
的长取得最小值的点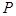 的坐标.
的坐标.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com