
【题目】给出下列命题中
① 非零向量![]() 满足
满足![]() ,则
,则![]() 的夹角为
的夹角为![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③若![]() 则
则![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为![]() .
.
以上命题正确的是 __________ (注:把你认为正确的命题的序号都填上)
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】[ ![]() ]表示不超过
]表示不超过 ![]() 的最大整数.若 S1=[
的最大整数.若 S1=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=3,
]=3,
S2=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=10,
]=10,
S3=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=21,
]=21,
…,
则Sn=( )
A.n(n+2)
B.n(n+3)
C.(n+1)2﹣1
D.n(2n+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数f(x)的局部对称点.
(1)若a∈R,a≠0,证明:函数f(x)=ax2+x﹣a必有局部对称点;
(2)若函数f(x)=2x+b在区间[﹣1,1]内有局部对称点,求实数b的取值范围;
(3)若函数f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
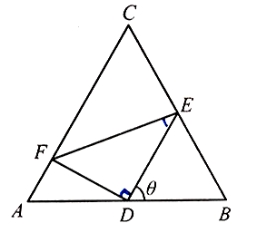
【题目】如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点,![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
(2)求![]() 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+3在(﹣∞,1]上是减函数,当x∈[a+1,1]时,f(x)的最大值与最小值之差为g(a),则g(a)的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2 ![]() .
. 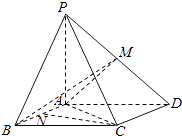
(1)求证:CD⊥平面PAC;
(2)如果如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据电影院的经营经验,当每张票价不超过10元时,票可全部售出;当票价高于10元时,每提高1元,将有30张票不能售出.为了获得更好的收益,需要给电影院一个合适的票价,基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放映一场电影的成本是5750元,票房收入必须高于成本.用x(元)表示每张票价,用y(元)表示该电影放映一场的纯收入(除去成本后的收入). (Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)票价定为多少时,电影放映一场的纯收入最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com