
【题目】圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】某校从参加高三期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及样本频率分布表如下:
分组 | 频数 | 频率 |
[40,50) | 2 | 0.04 |
[50,60) | 3 | 0.06 |
[60,70) | 14 | 0.28 |
[70,80) | 15 | ② |
[80,90) | ① | 0.24 |
[90,100] | 4 | 0.08 |
合计 | ③ | ④ |
(1)请把给出的样本频率分布表中的空格都填上;
(2)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学,已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组 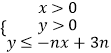 所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn , 记Dn内的格点(格点即横坐标和纵坐标皆为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记 ![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 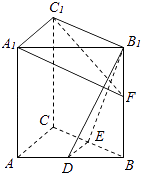
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知n∈N* , 设Sn是单调递减的等比数列{an}的前n项和,a1= ![]() 且S2+a2 , S4+a4 , S3+a3成等差数列.
且S2+a2 , S4+a4 , S3+a3成等差数列.
(1)求数列{an}的通项公式;
(2)记数列{nan}的前n项和为Tn , 求证:对于任意正整数n, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】虽然吸烟有害健康,但是由于历史以及社会的原因,吸烟也是部分公民交际的重要媒介.世界卫生组织1987年11月建议把每年的4月7日定为世界无烟日,且从1989年开始,世界无烟日改为每年的5月31日.某报社记者专门对吸烟的市民做了戒烟方面的调查,经抽样只有![]() 的烟民表示愿意戒烟,将频率视为概率.
的烟民表示愿意戒烟,将频率视为概率.
(1)从该市吸烟的市民中随机抽取3位,求至少有一位烟民愿意戒烟的概率;
(2)从该市吸烟的市民中随机抽取4位, ![]() 表示愿意戒烟的人数,求
表示愿意戒烟的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:函数f(x)= ![]() (a>0,且a≠1)在R上为单调递减函数,命题q:x∈[0,
(a>0,且a≠1)在R上为单调递减函数,命题q:x∈[0, ![]() ],x2﹣a≤0恒成立.
],x2﹣a≤0恒成立.
(1)求命题q真时a的取值范围;
(2)若命题p∧q为假,p∨q为真,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com