
如图,直三棱柱ABC A′B′C′,∠BAC=90°,AB=AC=
A′B′C′,∠BAC=90°,AB=AC= ,AA′=1,点M,N分别为
,AA′=1,点M,N分别为
A′B和B′C′的中点.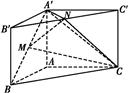
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′ MNC的体积.(锥体体积公式V=
MNC的体积.(锥体体积公式V=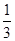 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
(1)见解析 (2)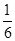
解析(1)证明:法一 连接AB′,AC′,如图所示,由已知∠BAC=90°,AB=AC,三棱柱ABC A′B′C′为直三棱柱,
A′B′C′为直三棱柱,
所以M为AB′的中点.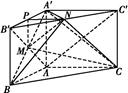
又因为N为B′C′的中点,
所以MN∥AC′.
又MN?平面A′ACC′,AC′?平面A′ACC′,
所以MN∥平面A′ACC′.
法二 取A′B′的中点P,连接MP,NP,AB′,如图所示,
因为M,N分别为AB′与B′C′的中点,
所以MP∥AA′,PN∥A′C′.
所以MP∥平面A′ACC′,PN∥平面A′ACC′.
又MP∩NP=P,所以平面MPN∥平面A′ACC′.
而MN?平面MPN,所以MN∥平面A′ACC′.
(2)解:连接BN,如图所示,
由题意知A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,
所以A′N⊥平面NBC.
又A′N= B′C′=1,
B′C′=1,
故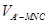 =
=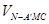 =
=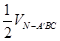 =
=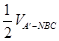 =
=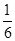 .
.


科目:高中数学 来源: 题型:解答题
如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC=3,侧面PBC⊥底面ABCD,O是BC的中点.
(1)求证:DC∥平面PAB;
(2)求四棱锥P﹣ABCD的体积.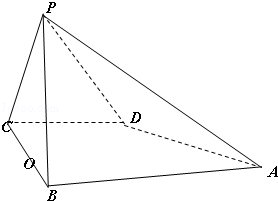
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知矩形 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
(1)求圆柱体的侧面积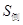 的值;
的值;
(2)若 是半圆弧
是半圆弧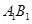 的中点,点
的中点,点 在半径
在半径 上,且
上,且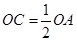 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在△ABC中,∠ABC=90°,∠A=30。,斜边AC上的中线BD=2,现沿BD将△BCD折起成三棱锥C-ABD,已知G是线段BD的中点,E,F分别是CG,AG的中点.
(1)求证:EF//平面ABC;
(2)三棱锥C—ABD中,若棱AC= ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在边长为a的正三角形铁皮的三个角切去三个全等的四边形,再把它的边沿虚线折起(如图),做成一个无盖的正三角形底铁皮箱,当箱底边长为多少时,箱子容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,BC=3.
(1)求证:AB1∥平面BC1D;
(2)求四棱锥B-AA1C1D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是某三棱柱被削去一个底面后的直观图与侧(左)视图、俯视图.已知CF=2AD,侧(左)视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.求该几何体的体积.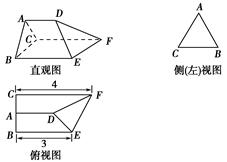
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com