
【题目】某手机厂商在销售某型号手机时开展“手机碎屏险”活动.用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费
元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例):
元时愿意购买该“手机碎屏险”的用户比例):

(1)根据上面的数据计算得![]() ,求出
,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若愿意购买该“手机碎屏险”的用户比例超过![]() ,则手机厂商可以获利,现从表格中的
,则手机厂商可以获利,现从表格中的![]() 种保费任取
种保费任取![]() 种,求这
种,求这![]() 种保费至少有一种能使厂商获利的概率.
种保费至少有一种能使厂商获利的概率.
附:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,![]()
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 和
和![]() 是两个边长为2的正三角形,
是两个边长为2的正三角形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
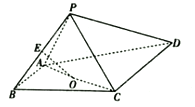
(1)证明:![]() 平面
平面![]() .
.
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局统计了我国近10年(2009年2018年)的GDP(GDP是国民经济核算的核心指标,也是衡量一个国家或地区总体经济状况的重要指标)增速的情况,并绘制了下面的折线统计图.

根据该折线统计图,下面说法错误的是
A. 这10年中有3年的GDP增速在9.00%以上
B. 从2010年开始GDP的增速逐年下滑
C. 这10年GDP仍保持6.5%以上的中高速增长
D. 2013年—2018年GDP的增速相对于2009年—2012年,波动性较小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,
,![]() 分别交直线
分别交直线![]() 于,
于,![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试问:
,试问:![]() 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 底面
底面![]() ,
,![]() 是棱
是棱![]() 的中点,且
的中点,且![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的大小;
的大小;
(3)如果![]() 是棱
是棱![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是棱长为2的正方体,
是棱长为2的正方体,![]() 为面对角线
为面对角线![]() 上的动点(不包括端点),
上的动点(不包括端点),![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,
,![]() 于
于![]() .
.

(1)试用反证法证明直线![]() 与
与![]() 是异面直线;
是异面直线;
(2)设![]() ,将
,将![]() 长表示为
长表示为![]() 的函数
的函数![]() ,并求此函数的值域;
,并求此函数的值域;
(3)当![]() 最小时,求异面直线
最小时,求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
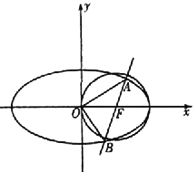
【题目】如图,椭圆G的中心在坐标原点,其中一个焦点为圆F:x2+y2﹣2x=0的圆心,右顶点是圆F与x轴的一个交点.已知椭圆G与直线l:x﹣my﹣1=0相交于A、B两点.
(I)求椭圆的方程;
(Ⅱ)求△AOB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com