
分析 (Ⅰ)设{an}的公差为d,运用等差数列的通项公式和求和公式,以及定义,解得d=2,进而得到通项公式;
(Ⅱ)由(Ⅰ)知:${b_n}=\frac{1}{{({2n-1})({2n+3})}}=\frac{1}{4}({\frac{1}{2n-1}-\frac{1}{2n+3}})$.运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
解答 解:(Ⅰ)设{an}的公差为d,由a1=1,an=1+(n-1)d=nd+1-d,
若$\left\{{\frac{S_n}{n}}\right\}$为公差是1的等差数列,
则$\frac{{S}_{n}}{n}$=$\frac{1}{2}$nd+1-$\frac{1}{2}$d,
当n≥2时,$\frac{{S}_{n}}{n}$-$\frac{{S}_{n-1}}{n-1}$=$\frac{1}{2}$d=1,解得d=2,
则an=2n-1,n∈N*;
(Ⅱ)由(Ⅰ)知:${b_n}=\frac{1}{{({2n-1})({2n+3})}}=\frac{1}{4}({\frac{1}{2n-1}-\frac{1}{2n+3}})$.
∴${T_n}=\frac{1}{4}({1-\frac{1}{5}+\frac{1}{3}-\frac{1}{7}+\frac{1}{5}-\frac{1}{9}+…+\frac{1}{2n-1}-\frac{1}{2n+3}})$=$\frac{1}{4}({\frac{4}{3}-\frac{1}{2n+1}-\frac{1}{2n+3}})$
=$\frac{1}{3}-\frac{n+1}{{({2n+1})({2n+3})}}$(n∈N*).
点评 本题考查等差数列的通项公式和求和公式的运用,考查方程思想,以及数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
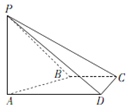 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,AD=2BC=2CD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,AD=2BC=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2kπ}{3}-\frac{π}{9}$,$\frac{2kπ}{3}+\frac{2π}{9}$),k∈Z | B. | ($\frac{2kπ}{3}$-$\frac{4π}{9}$,$\frac{2kπ}{3}$-$\frac{π}{9}$),k∈Z | ||
| C. | ($\frac{2kπ}{3}$+$\frac{π}{18}$,$\frac{2kπ}{3}$+$\frac{7π}{18}$),k∈Z | D. | ($\frac{2kπ}{3}$-$\frac{7π}{18}$,$\frac{2kπ}{3}-\frac{π}{18}$),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有5人.
在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有5人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com