
A.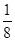 | B.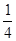 | C.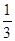 | D.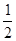 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
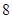 个等级,等级系数
个等级,等级系数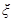 依次为
依次为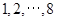 ,其中
,其中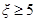 为标准
为标准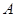 ,
, 为标准
为标准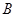 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准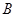 生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取
生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下: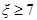 的为一等品,等级系数
的为一等品,等级系数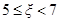 的为二等品,等级系数
的为二等品,等级系数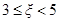 的为三等品.
的为三等品.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
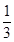 ,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为A.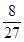 | B.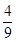 |
C.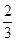 | D.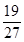 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
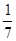 ,现在甲乙两人轮流从袋中摸出一球,甲先取,乙后取,然后甲再取…取后不放回,直到两人中有一人取到白球时即终止,每个球每一次被取到的机会是均等的,那么甲取到白球的概率是 ( )
,现在甲乙两人轮流从袋中摸出一球,甲先取,乙后取,然后甲再取…取后不放回,直到两人中有一人取到白球时即终止,每个球每一次被取到的机会是均等的,那么甲取到白球的概率是 ( )A.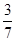 | B.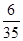 | C.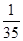 | D.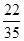 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
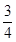 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡。
持银卡。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
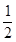 ,乙能解决它的概率为
,乙能解决它的概率为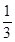 ,两人试图独立地在半小时内解决它,求:
,两人试图独立地在半小时内解决它,求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
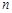 个白球,从中任取2个球.
个白球,从中任取2个球.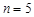 ,求取到的2个球恰好是一个红球和一个白球的概率;
,求取到的2个球恰好是一个红球和一个白球的概率;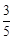 ,求
,求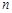 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com