
已知,A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于EF两点,交抛物线于M、N两点,交y轴于B、C两点
(1)当A点坐标为(8,4)时,求直线EF的方程;
(2)当A点坐标为(2,2)时,求直线MN的方程;
(3)当A点的横坐标大于2时,求△ABC面积的最小值。
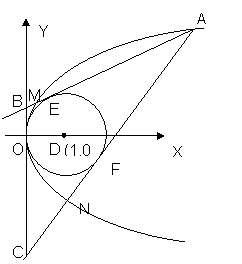
(1)∵DEFA四点共圆 EF是圆(x-1)2+y2=1及(x-1)(x-8)+y(y-4)=0
的公共弦 ∴EF的方程为7x+4y-8=0
(2)设AM的方程为y-2=k(x-2)
即kx-y+2-2k=0与圆(x-1)2+y2=1相切得![]() =1
=1
∴k=![]() 把y-2=
把y-2=![]() (x-2)代入y2=2x得M(
(x-2)代入y2=2x得M(![]() ,
,![]() ),而N(2,-2)
),而N(2,-2)
∴MN的方程为3x+2y-2=0
(3)设P(x0,y0),B(0,b),C(0,c),不妨设b>c, 直线PB的方程为y-b=![]() ,
,
即(y0-b)x-x0y+x0b=0又圆心(1,0)到PB的距离为1,
所以![]() =1,故(y0-b)2+x
=1,故(y0-b)2+x![]() =(y0-b)2+2x0b(y0-b)+ x
=(y0-b)2+2x0b(y0-b)+ x![]() b2
b2
又x0>2,上式化简得(x0-2)b2+2y0b-x0=0 同理有(x0-2)c2+2y0c-x0=0
故b,c是方程(x0-2)t2+2y0t-x0=0的两个实数根
所以b+c=![]() ,bc=
,bc=![]() ,则(b-c)2=
,则(b-c)2=![]()
因为P(x0,y0)是抛物线上的点,所以有y![]() =2x0,则
=2x0,则
(b-c)2=![]() ,b-c=
,b-c=![]() ,
,
∴S△PBC=![]() (b-c)x0=
(b-c)x0=![]() =x0-2+
=x0-2+![]() +4≥2
+4≥2![]() +4=8
+4=8
当(x0-2)2=4时,上式取等号,此时x0=4,y=±2![]() ,因此S△PBC的最小值为8
,因此S△PBC的最小值为8


科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
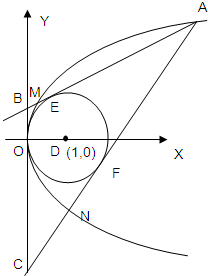 (2011•钟祥市模拟)已知,A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于EF两点,交抛物线于M.N两点,交y轴于B.C两点
(2011•钟祥市模拟)已知,A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于EF两点,交抛物线于M.N两点,交y轴于B.C两点查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
|
(1)求p的值;
(2)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦
的中点分别为G,H.求|GH|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分) 已知点A是抛物线y2=2px(p>0)上一点,F为抛物线的焦点,准线l与x轴交于点K, 已知|AK|=![]() |AF|,三角形AFK的面积等于8. (Ⅰ)求p的值;(Ⅱ)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦的中点分别为G,H.求|GH|的最小值.
|AF|,三角形AFK的面积等于8. (Ⅰ)求p的值;(Ⅱ)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦的中点分别为G,H.求|GH|的最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省、钟祥一中高三第二次联考数学理卷 题型:解答题
(13分)已知,A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于EF两点,交抛物线于M.N两点,交y轴于B.C两点
(1)当A点坐标为(8,4)时,求直线EF的方程;
(2)当A点坐标为(2,2)时,求直线MN的方程;
(3)当A点的横坐标大于2时,求△ABC面积的最小值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com