
分析 由题意,结合点斜式方程可得,f(x)的导数为f′(x)=(x-1)(x2-4),令导数小于0,运用二次不等式的解法,计算即可得到所求减区间.
解答 解:由图象上任意一点(x0,y0)处的切线方程为
y=(x0-1)(x02-4)(x-x0)+f(x0),
由点斜式方程可得,
f(x)的导数为f′(x)=(x-1)(x2-4),
由f′(x)<0,即$\left\{\begin{array}{l}{x-1>0}\\{{x}^{2}-4<0}\end{array}\right.$或$\left\{\begin{array}{l}{x-1<0}\\{{x}^{2}-4>0}\end{array}\right.$,
即有$\left\{\begin{array}{l}{x>1}\\{-2<x<2}\end{array}\right.$或$\left\{\begin{array}{l}{x<1}\\{x>2或x<-2}\end{array}\right.$,
即1<x<2或x<-2.
故答案为:(-∞,-2)∪(1,2).
点评 本题考查导数的运用:求单调区间,注意运用二次不等式的解法,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
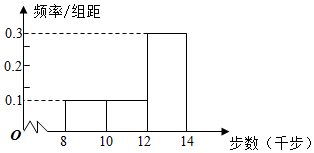 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,AD,DE是⊙O的切线.AD,BE的延长线交于点C.
如图,AB是⊙O的直径,AD,DE是⊙O的切线.AD,BE的延长线交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com