
ijУ�Ӹ߶��꼶ѧ���������ȡ60��ѧ�����������п��Ե����γɼ�����Ϊ�������ֳ����Σ�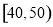 ��
��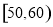 ������
������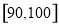 ��õ�����Ƶ�ʷֲ�ֱ��ͼ��
��õ�����Ƶ�ʷֲ�ֱ��ͼ��
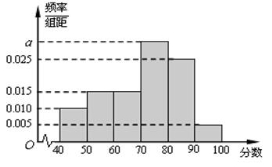
�����������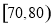 �ڵ�Ƶ�ʣ�
�ڵ�Ƶ�ʣ�
������Ƶ�ʷֲ�ֱ��ͼ�����Ƹ�У�߶��꼶ѧ�����п������γɼ���ƽ���֡���������λ������С�������һλ��Ч���֣�
�����÷ֲ�����ķ����ڸ������ε�ѧ���г�ȡһ������Ϊ20����������������γ�ȡ�������ֱ��Ƕ��٣�
 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ�ϲ��и߶�����ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
����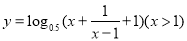 ��ֵ���ǣ� ��
��ֵ���ǣ� ��
A��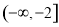 B��
B��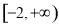 C��
C��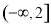 D��
D��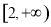
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com