
分析 (1)动点M(x,y)到点F(3,0)的距离比点M到直线x+4=0的距离小1,可知:动点M(x,y)到点F(3,0)的距离与到直线x+3=0的距离相等.根据抛物线的定义可知:点M的轨迹是以F(3,0)为焦点,x=-3为准线的抛物线,即可得出;
(2)通过设A(x1,y1)、B(x2,y2)可知(y1+y2)(y1-y2)=12(x1-x2),利用直线AB的斜率为-4可知可知AB中点的坐标,计算即得结论.
解答 解:(1)∵动点M(x,y)到点F(3,0)的距离比点M到直线x+4=0的距离小1,
∴动点M(x,y)到点F(3,0)的距离与到直线x+3=0的距离相等.
根据抛物线的定义可知:点M的轨迹是以F(3,0)为焦点,x=-3为准线的抛物线,
∴y2=4×3x,即y2=12x….(4分)
(2)设A(x1,y1),B(x2,y2),
则代入作差,可得(y1+y2)(y1-y2)=12(x1-x2),
又∵直线AB的斜率为-4,
∴-4(y1+y2)=12,
∴AB中点的坐标为($\frac{7}{2}$,-$\frac{3}{2}$),
∴直线AB的方程为:y+$\frac{3}{2}$=-4(x-$\frac{7}{2}$),即4x+y-$\frac{45}{2}$=0,
经检验,此时直线AB与抛物线有两个不同的交点,满足题意.
点评 本题考查了抛物线的定义,考查点差法,考查运算求解能力,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|-2≤x<1} | C. | {x|-2≤x≤1} | D. | {x|-2<x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果直线m∥平面α,直线n?α内,那么m∥n | |
| B. | 如果平面α⊥平面β,任取直线m?α,那么必有m丄β | |
| C. | 若直线m∥平面α,直线n∥平面α,则m∥n | |
| D. | 如果平面a外的一条直线m垂直于平面a内的两条相交直线,那么m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是线段CC1的中点,连接AE,B1E,AB1,B1C,BC1,得到的图形如图所示.
已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是线段CC1的中点,连接AE,B1E,AB1,B1C,BC1,得到的图形如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
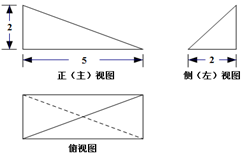
| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{25}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com