
����Ŀ�������������⣺
����֪����A={1��a}��B={1��2��3}����a=3���ǡ�AB���ij�ֲ���Ҫ������
�ڡ�x��0���ǡ�ln��x+1����0���ı�Ҫ�����������
�ۡ�����f��x��=cos2ax��sin2ax����С������Ϊ�С��ǡ�a=1���ij�Ҫ������
�ܡ�ƽ������ ![]() ��
�� ![]() �ļн��Ƕ۽ǡ��ij�Ҫ�����ġ�
�ļн��Ƕ۽ǡ��ij�Ҫ�����ġ� ![]()
![]() ��0����
��0����
������ȷ��������������������ȷ�������Ŷ�д�ϣ�
���𰸡��٢�
���������⣺���ڢ٣���a=3ʱ��A={1��a}={1��3}������AB����AB����a=2��3��
�ࡰa=3���ǡ�AB���ij�ֲ���Ҫ�������ʢ���ȷ��
���ڢڣ���x��0����x+1��1����x+1��0ʱ��ln��x+1����0��
��ln��x+1����0����0��x+1��1���ੁ1��x��0����x��0��
�ࡰx��0����ln��x+1����0�ı�Ҫ������������ʢ���ȷ��
���ڢۣ�����f��x��=cos2ax��sin2ax=cos2ax����С������Ϊ�У�
�� ![]() =�У�|a|=1����ã�a=��1���ʳ���Բ�������
=�У�|a|=1����ã�a=��1���ʳ���Բ�������
��֮����a=1����f��x��=cos2x��sin2x=cos2x����С������Ϊ�У���Ҫ�Գ�����
�ʺ���f��x��=cos2ax��sin2ax����С������Ϊ���ǡ�a=1���ı�Ҫ������������ʢ۴���
���ڢܣ�����ƽ������ ![]() ��
�� ![]() �ļн��Ƕ۽ǡ�ʱ����
�ļн��Ƕ۽ǡ�ʱ���� ![]()
![]() ��0����
��0����
��֮����������������������ʱ���� ![]()
![]() ��0�����ʢܴ���
��0�����ʢܴ���
����ȷ���������ǣ��٢ڣ�
���Դ��ǣ��٢ڣ�
�����㾫����������Ĺؼ������������������ж���Ӧ�õ����֪ʶ�������������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������¡���ҵ�����и����Ϣ���һλ��ѧ��ҵ����������ҵ�������г����С����㣬�����������ɹ�ѡ��
����1������һ���Ƽ�С��ҵ����Ҫһ���Դ���40��Ԫ����һ������Ǵ�����10%���Ժ�ÿ�����һ������25%������
����2������һ��ʳƷС�꣬��Ҫһ���Դ���20��Ԫ����һ������Ǵ�����15%���Ժ�ÿ�����һ����������1.5��Ԫ�����ַ���ʹ��������10�꣬����һ���Ի�����Ϣ�����ַ���������Ϣ2%�ĸ������㣨�ο����ݣ�1.259=7.45��1.2510=9.3��1.029=1.20��1.0210=1.22����
��1��10�����1������2��������ֱ��ж�����Ԫ��
��2��10�����һ�ַ���������ϴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017���ո�����ģ��һ��ҵ��ij�������������ȡ![]() ����Ʒ��������Щ��Ʒ��ij���ָ��ֵ
����Ʒ��������Щ��Ʒ��ij���ָ��ֵ![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ.
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ.
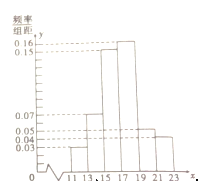
��1�����Ƹü���ָ��ֵ![]() ƽ����
ƽ����![]() ��
��
��2����ֱ��ͼ�ļ���ָ��ֵ�����У���![]() ����������Ƶ����Ϊ
����������Ƶ����Ϊ![]() ȡ������ֵ��Ƶ�ʣ���
ȡ������ֵ��Ƶ�ʣ���![]() �����Ʒ���ϸ��ָ���ҵÿ��Ӹ��������������ȡ
�����Ʒ���ϸ��ָ���ҵÿ��Ӹ��������������ȡ![]() ����Ʒ��⣬�Dz��ϸ��Ʒ�ĸ���Ϊ
����Ʒ��⣬�Dz��ϸ��Ʒ�ĸ���Ϊ![]() ����
����![]() ����ѧ����
����ѧ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բmx2+ny2=1��ֱ��x+y��1=0�ཻ��A��B���㣬��AB�е�M������ԭ���ֱ�ߵ�б��Ϊ ![]() ����
���� ![]() ��ֵΪ�� ��
��ֵΪ�� ��
A.![]()
B.![]()
C.1
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��A��2��4����ֱ��l��x��2y+1=0��
��1�������A��ƽ����l��ֱ�ߵķ��̣�
��2������M��ֱ��l�ϣ���AM��l�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() ����������
����������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����֪
����֪![]() ��
��![]() ��
��![]() .
.
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2��֤������һ��������![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��������16��)
�躯��![]() .
.
��1����![]() =1ʱ������
=1ʱ������![]() ȡ��Сֵ����ʵ��
ȡ��Сֵ����ʵ��![]() ��ֵ��
��ֵ��
��2��������![]() �ڶ��������ǵ�����������ʵ��
�ڶ��������ǵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��֤��������������
��֤��������������![]() ������ʽ
������ʽ![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����g��x������g��x��=g�䣨1��ex��1��g��0��x+ ![]() ���Ҵ���ʵ��x0ʹ�ò���ʽ2m��1��g��x0����������m��ȡֵ��ΧΪ�� ��
���Ҵ���ʵ��x0ʹ�ò���ʽ2m��1��g��x0����������m��ȡֵ��ΧΪ�� ��
A.�����ޣ�2]
B.�����ޣ�3]
C.[1��+�ޣ�
D.[0��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c��a=btanA����BΪ�۽ǣ�
��1����B��A��ֵ��
��2����sinA+sinC��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com