
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,其中点
,其中点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
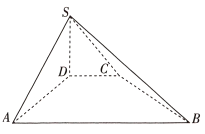
(1)证明:![]() 平面
平面![]() .
.
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接![]() ,
,![]() ,根据直径所对圆周角是直角,得到
,根据直径所对圆周角是直角,得到![]() ,计算出
,计算出![]() 的长,通过勾股定理证得
的长,通过勾股定理证得![]() ,再根据面面垂直的性质定理得到
,再根据面面垂直的性质定理得到![]() 平面
平面![]() .(2)
.(2)![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() ,
,![]() ,
,![]() 轴的正方向建立空间直角坐标系通过计算平面
轴的正方向建立空间直角坐标系通过计算平面![]() 和平面
和平面![]() 的法向量,计算二面角
的法向量,计算二面角![]() 的余弦值,进而求得其正弦值.
的余弦值,进而求得其正弦值.
(1)证明:连接![]() ,
,![]() ,因为点
,因为点![]() 在以
在以![]() 为直径的圆上,所以
为直径的圆上,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() .
.
因为![]() 为等腰梯形,
为等腰梯形,![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() ,从而得
,从而得![]() .
.
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
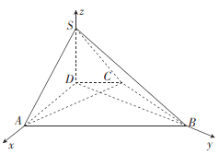
(2)解:由(1)易知![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() ,
,![]() ,
,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
由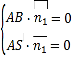 ,得
,得 ,令
,令![]() ,得
,得![]() ,
,
由 ,得
,得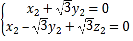 ,令
,令![]() ,得
,得![]() ,
,
所以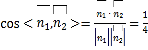 ,所以
,所以![]() ,
,
故二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】网约车的兴起丰富了民众出行的选择,为民众出行提供便利的同时也解决了很多劳动力的就业问题,据某著名网约车公司“滴滴打车”官网显示,截止目前,该公司已经累计解决退伍军人转业为兼职或专职司机三百多万人次,梁某即为此类网约车司机,据梁某自己统计某一天出车一次的总路程数可能的取值是20、22、24、26、28、![]() ,它们出现的概率依次是
,它们出现的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求这一天中梁某一次行驶路程X的分布列,并求X的均值和方差;
(2)网约车计费细则如下:起步价为5元,行驶路程不超过![]() 时,租车费为5元,若行驶路程超过
时,租车费为5元,若行驶路程超过![]() ,则按每超出
,则按每超出![]() (不足
(不足![]() 也按
也按![]() 计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n为平面α外两条直线,其在平面α内的射影分别是两条直线m1和n1,给出下列4个命题:①m1∥n1m∥n;②m∥nm1与n1平行或重合;③m1⊥n1m⊥n;④m⊥nm1⊥n1.其中所有假命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
表![]()
图![]()
(I)根据表![]() ,是否有
,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
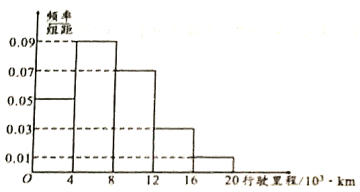
(II)图![]() 给出的是
给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(III)用表![]() 中的频率估计概率,随机调查
中的频率估计概率,随机调查![]() 名
名![]() 岁以下车主,设其中购买了轿车的人数为
岁以下车主,设其中购买了轿车的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个不同的红球和
个不同的红球和![]() 个不同的白球,放入同一个袋中,现从中取出
个不同的白球,放入同一个袋中,现从中取出![]() 个球.
个球.
(1)若取出的红球的个数不少于白球的个数,则有多少种不同的取法;
(2)取出一个红球记![]() 分,取出一个白球记
分,取出一个白球记![]() 分,若取出
分,若取出![]() 个球的总分不少于
个球的总分不少于![]() 分,则有多少种不同的取法;
分,则有多少种不同的取法;
(3)若将取出的![]() 个球放入一箱子中,记“从箱子中任意取出
个球放入一箱子中,记“从箱子中任意取出![]() 个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到
个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到![]() 个红球并且恰有一次取到
个红球并且恰有一次取到![]() 个白球的概率.
个白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,A(0,1),AB边上的高CD所在直线的方程为x+2y-4=0,AC边上的中线BE所在直线的方程为2x+y-3=0.
(1)求直线AB的方程;
(2)求直线BC的方程;
(3)求△BDE的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直接坐标系![]() 中,直线l的方程为x-y+4=0,曲线C的参数方程为
中,直线l的方程为x-y+4=0,曲线C的参数方程为![]() .
.
(I)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com