
【题目】若函数![]() 是
是![]() 上的单调减函数,已知
上的单调减函数,已知![]() ,
,![]() ,且
,且![]() 在定义域内恒成立,则实数
在定义域内恒成立,则实数![]() 的取值范围为______.
的取值范围为______.
【答案】![]() 或
或![]()
【解析】
先由函数单调递减得到m的值,将函数g(x)初步简化,然后针对函数h(x)中的参数n分类讨论,目的是为了将不等式简化,以便于能利用导数工具求解.
由函数f(x)=﹣4x3﹣mx2+(3﹣m)x+1是R上的单调减函数,
则可知f'(x)=﹣12x2﹣2mx+3﹣m≤0在R上恒成立,
△=4m2﹣4×(﹣12)×(3﹣m)=4(m﹣6)2≤0,故m=6,
则函数g(x)=lnx﹣2nx,由题可知![]() 在定义域(0,+∞)内恒成立,
在定义域(0,+∞)内恒成立,
①当n≥0时,函数![]() 恒成立,故原不等式可转化为g(x)=lnx﹣2nx≤0恒成立,
恒成立,故原不等式可转化为g(x)=lnx﹣2nx≤0恒成立,
![]() ,
,
令g'(x)=0,解得![]() ,
,
则在![]() 上,g'(x)>0,g(x)单调递增,
上,g'(x)>0,g(x)单调递增,
在![]() 上,g'(x)<0,g(x)单调递减,
上,g'(x)<0,g(x)单调递减,
则![]() ,
,
则ln2n≥﹣1=lne﹣1,即![]()
满足前提n≥0,故![]()
②当n<0时,令![]() ,解得
,解得![]() ,
,
则当![]() 时,
时,![]() ,g(x)h(x)≤0恒成立
,g(x)h(x)≤0恒成立
可转化为g(x)=lnx﹣2nx≤0恒成立,
![]() ,则g(x)在(0,+∞)上单调递增,
,则g(x)在(0,+∞)上单调递增,
故在![]() 上也单调递增,
上也单调递增,
则![]() ,解得n≤﹣e2;
,解得n≤﹣e2;
当![]() 时,
时,![]() ,g(x)h(x)≤0恒成立
,g(x)h(x)≤0恒成立
可转化为g(x)=lnx﹣2nx≥0恒成立,
由上可知,g(x)在![]() 上单调递增,
上单调递增,
故![]() ,解得n≥﹣e2,即﹣e2≤n<0;
,解得n≥﹣e2,即﹣e2≤n<0;
要使得两种情形下都能恒成立,则取其交集得到,n=﹣e2,
综上所述,可得要使得g(x)h(x)≤0在定义域内恒成立,
则实数n的取值范围为![]() .
.
故答案为:![]() 或
或![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
(1)求椭圆C的方程;
(2)过椭圆C的左顶点A作直线m,与圆O相交于两点R,S,若△ORS是钝角三角形,求直线m的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的长轴长
的长轴长![]() ,短轴长
,短轴长![]() .
.

(1)求椭圆的方程;
(2)记椭圆的左右顶点![]() ,分别过
,分别过![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,
,![]() 为 椭圆上位于
为 椭圆上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
(i)当直线![]() 的斜率为2时,求
的斜率为2时,求![]() 的面积;
的面积;
(ii)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.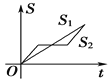 B.
B.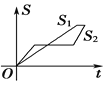 C.
C.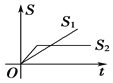 D.
D.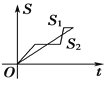
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com