Question

【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本称出它们的质量(单位：克)，质量值落在的产品为合格品，否则为不合格品.如表是甲流水线样本频数分布表，如图是乙流水线样本的频率分布直方图.

产品质量/克	频数
(490，495]	6
(495，500]	8
(500，505]	14
(505，510]	8
(510，515]	4

甲流水线样本频数分布表:

	甲流水线	乙流水线	总计
合格品
不合格品
总计

（1）根据上表数据作出甲流水线样本的频率分布直方图；

（2）若以频率作为概率，试估计从乙流水线任取件产品，该产品恰好是合格品的概率；

（3）由以上统计数据完成下面列联表，能否在犯错误的概率不超过的前提下认为产品的包装质量与两条自动包装流水线的选择有关？

附表：

（参考公式： ）

Answer 1

【答案】（1）直方图见解析；（2） ；（3）能.

【解析】试题分析：（1）根据所给的每一组的频数和样本容量做出每一组的频率，可在平面直角坐标系中做出频率分步直方图；（2）根据直方图的性质，可得直方图中中间三个矩形的面积之和即为产品恰好是合格品的概率；（3）利用公式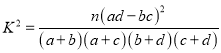求得 ，与邻界值比较，即可得到结论；

试题解析：（1）根据所给的每一组的频数和样本容量做出每一组的频率，在平面直角坐标系中做出频率分步直方图，甲流水线样本的频率分布直方图如下：

（2）由图1知，乙样本中合格品数为（0.06+0.09+0.03）×5×40=36，故合格品的频率为36/40=0.9据此可估计从乙流水线上任取一件产品该产品为合格品的概率P=0.9.

（3）

	甲流水线	乙流水线	总计
合格品	30	36	66
不合格品	10	4	14
总计	40	40	80

,能在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关.