
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①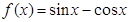 ;②
;②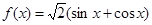 ;③
;③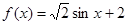 ;④
;④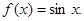 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )
A.①② B.①③ C.③④ D.②④
B
【解析】
试题分析:根据题意,两个y=Asin(ωx+∅)+b 型函数互为生成的函数的条件是,这两个函数的解析式中的A和ω相同,∵①f(x)=sinx-cosx=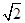 sin(x-
sin(x-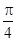 ),②f(x)=
),②f(x)=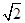 (sinx+cosx)=2sin(x+
(sinx+cosx)=2sin(x+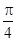 ),③f(x)=
),③f(x)=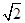 sinx+2,④f(x)=sinx.故①③两个函数解析式中的A和ω相同,故这两个函数的图象通过平移能够完全重合.故①③互为生成的函数,故选B.
sinx+2,④f(x)=sinx.故①③两个函数解析式中的A和ω相同,故这两个函数的图象通过平移能够完全重合.故①③互为生成的函数,故选B.
考点:本试题主要考查了函数y=Asin(ωx+∅)+b 的图象变换,应用了此函数图象在平移过程中A和ω不变.
点评:解决该试题的关键利用函数y=Asin(ωx+∅)+b 的图象在平移过程中A和ω一定不变.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
| A、①② | B、①③ | C、③④ | D、②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
| 3 |
| A、①② | B、①④ | C、②③ | D、③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com