
(本小题满分12分)
已知:函数y=f (x)的定义域为R,且对于任意的a,b∈R,都有f (a+b)=f (a)+f (b),且当x>0时,f (x)<0恒成立.
证明:(1)函数y=f (x)是R上的减函数.
(2)函数y=f (x)是奇函数.
解析试题分析:(1)设x1>x2,则x1-x2>0,而f (a+b)=f (a)+f (b),
所以f (x1)=f (x1-x2+x2)=f (x1-x2)+f (x2)<f (x2),
即f (x1)<f (x2),所以函数在R上是减函数. ……6分
(2)由f (a+b)=f (a)+f (b)得:f (x-x)=f (x)+f (-x),即f (x)+f (-x)=f (0),而f (0)=0,
所以f (-x)=-f (x),即函数f (x)是奇函数. ……12分
考点:本题考查抽象函数及其应用;函数奇偶性的判断.函数的单调性。
点评:本题以抽象函数的单调性证明为载体考查了函数的奇偶性的定义,其中利用“凑配法”得到f(0)=0及f(-x)=-f(x)是解答的关键.


科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知方程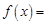
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求:
(Ⅰ)若方程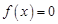 的根为一正一负,则求实数
的根为一正一负,则求实数 的取值范围;
的取值范围;
(Ⅱ)若方程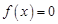 的两根都在
的两根都在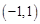 内,则求实数
内,则求实数 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分) 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB= (
( >2),BC=2,且AE=AH=CF=CG,设AE=
>2),BC=2,且AE=AH=CF=CG,设AE=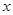 ,绿地面积为
,绿地面积为 .
.
(1)写出 关于
关于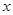 的函数关系式,并指出这个函数的定义域;
的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积 最大? (10分)
最大? (10分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com