
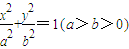 的内接等腰△ABC的顶点A的坐标为(0,b),其底边BC上的高在y轴上,若△ABC的面积不超过
的内接等腰△ABC的顶点A的坐标为(0,b),其底边BC上的高在y轴上,若△ABC的面积不超过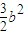 ,则椭圆离心率的取值范围为( )
,则椭圆离心率的取值范围为( )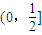
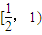
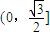
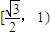
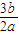 ,再根据c2=a2-b2,就能得到答案.
,再根据c2=a2-b2,就能得到答案.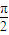 <x<
<x<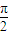 .
.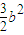
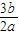
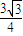 ≤
≤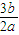
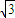 a≤2b
a≤2b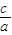 ≤
≤ .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:高考数学一轮复习必备(第97-99课时):第十三章 导数-导数的应用(2)(解析版) 题型:解答题
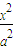 +
+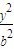 =1,(a>b>0)的长轴为AB,以AB为底边作椭圆的内接等腰梯形ABCD,求此等腰梯形面积的最大值.
=1,(a>b>0)的长轴为AB,以AB为底边作椭圆的内接等腰梯形ABCD,求此等腰梯形面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com