
| A. | $\overrightarrow{AB}•\overrightarrow{AQ}$ | B. | $\overrightarrow{AC}•\overrightarrow{AQ}$ | C. | $\overrightarrow{AD}•\overrightarrow{AQ}$ | D. | $\overrightarrow{AE}•\overrightarrow{AQ}$ |
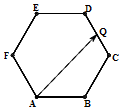
分析 由题意画出图形,然后以FC所在直线为x轴,以FC的中垂线为y轴建立平面直角坐标系,求出所用点的坐标,得到向量的坐标,求其数量积得答案.
解答 解:设正六边形的边长为2,以FC所在直线为x轴,以FC的中垂线为y轴建立平面直角坐标系,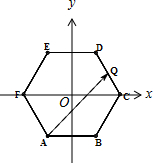
则A(-1,$-\sqrt{3}$),B(1,-$\sqrt{3}$),C(2,0),D(1,$\sqrt{3}$),E(-1,$\sqrt{3}$),Q($\frac{3}{2},\frac{\sqrt{3}}{2}$).
$\overrightarrow{AB}=(2,0)$,$\overrightarrow{AC}=(3,\sqrt{3})$,$\overrightarrow{AD}=(2,2\sqrt{3})$,$\overrightarrow{AE}=(0,2\sqrt{3})$,$\overrightarrow{AQ}=(\frac{5}{2},\frac{3\sqrt{3}}{2})$.
则$\overrightarrow{AB}•\overrightarrow{AQ}$=5,$\overrightarrow{AC}•\overrightarrow{AQ}$=12,$\overrightarrow{AD}•\overrightarrow{AQ}$=14,$\overrightarrow{AE}•\overrightarrow{AQ}$=9.
∴$\overrightarrow{AD}•\overrightarrow{AQ}$最大.
故选:C.
点评 本题考查平面向量的数量积运算,考查了数量积的坐标运算,建系起到事半功倍的效果,是中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
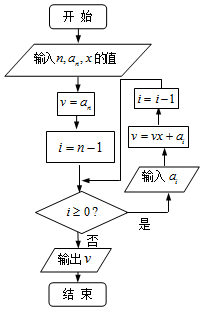 如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )
如图程序框图的算法思路,源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法,执行该程序框图,若输入的n,an,x分别为5,1,-2,且a4=5,a3=10,a2=10,a1=5,a0=1,则输出的v=( )| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或$-\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$或$-\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$或$-\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$或$\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实,黄实,利用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2,设勾股中勾股比为1:$\sqrt{3}$,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实,黄实,利用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2,设勾股中勾股比为1:$\sqrt{3}$,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )| A. | 866 | B. | 500 | C. | 300 | D. | 134 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-y2=1 | B. | y2-x2=1 | C. | y2-x2=2 | D. | x2-y2=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com