
【题目】集成电路E由3个不同的电子元件组成,现由于元件老化,3个电子元件能正常工作的概率分别降为![]() ,
,![]() ,
,![]() ,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。
,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。
(Ⅰ)求集成电路E需要维修的概率;
(Ⅱ)若某电子设备共由2个集成电路E组成,设X为该电子设备需要维修集成电路所需费用。求X的分布列和均值.
【答案】(Ⅰ) 集成电路E需要维修的概率为p1+p2=![]() +
+![]() =
=![]() ;(Ⅱ) E(X)=
;(Ⅱ) E(X)=![]() .
.
【解析】试题分析:(Ⅰ)设“三个电子元件能正常工作”分别记为事件A,B,C,则![]() ,
,![]() ,
,![]() ,依题意,集成电路E需要维修有两种情形:①3个元件都不能正常工作,②3个元件2个不能正常工作,由此能求出集成电路E需要维修的概率;(Ⅱ) 由题意知
,依题意,集成电路E需要维修有两种情形:①3个元件都不能正常工作,②3个元件2个不能正常工作,由此能求出集成电路E需要维修的概率;(Ⅱ) 由题意知![]() 的可能取值为0,100,200,分别求出相应的概率,由此能求出
的可能取值为0,100,200,分别求出相应的概率,由此能求出![]() 的分布列和
的分布列和![]() .
.
试题解析:(Ⅰ)设“三个电子元件能正常工作”分别记为事件A,B,C,则P(A)=![]() ,
,
P(B)=![]() ,P(C)=
,P(C)=![]() .
.
依题意,集成电路E需要维修有两种情形:
①3个元件都不能正常工作,概率为p1=P(![]() )=P(
)=P(![]() )P(
)P(![]() )P(
)P(![]() )=
)=![]() .
.
②3个元件2个不能正常工作,概率为
p2=P(![]() )+P(
)+P(![]() )+P(
)+P(![]() )=
)=![]() +
+![]() +
+![]() =
=![]() .
.
所以,集成电路E需要维修的概率为p1+p2=![]() +
+![]() =
=![]() .
.
(Ⅱ)P(X=0)=(1-![]() )2=
)2=![]() ,P(X=100)=
,P(X=100)=![]() ·
·![]() ·(1-
·(1-![]() )=
)=![]() ,P(X=200)=(
,P(X=200)=(![]() )2=
)2=![]() .
.
X的分布列为:
X | 0 | 100 | 200 |
P |
|
|
|
所以E(X)=0×![]() +100×
+100×![]() +200×
+200×![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】以下四个命题:
①对立事件一定是互斥事件;
②函数![]() 的最小值为2;
的最小值为2;
③八位二进制数能表示的最大十进制数为256;
④在![]() 中,若
中,若![]() ,
, ![]() ,
, ![]() ,则该三角形有两解.
,则该三角形有两解.
其中正确命题的个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间 | 2014年下半年 | 2015年上半年 | 2015年下半年 | 2016年上半年 | 2016年下半年 |
时间代号 |
|
|
|
|
|
人均读书量 |
|
|
|
|
|
根据散点图,可以判断出人均读书量![]() 与时间代号
与时间代号![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
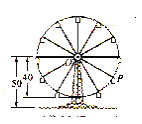
【题目】如图所示,摩天轮的半径为![]() 米,点
米,点![]() 距地面高度为
距地面高度为![]() 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每![]() 分钟转一圈,以点
分钟转一圈,以点![]() 为原点,过点
为原点,过点![]() 且平行与地平线的直线为
且平行与地平线的直线为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,设点
,设点![]() 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻![]() (分钟)时点
(分钟)时点![]() 距地面的高度
距地面的高度![]() (米),则
(米),则![]() 与
与![]() 的函数关系式
的函数关系式
![]()
![]() __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点![]() 到地面的距离不小于
到地面的距离不小于![]() 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() 和点
和点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线方程.
的切线,求切线方程.
(3)设直线![]() ,且直线
,且直线![]() 被圆
被圆![]() 所截得的弦为
所截得的弦为![]() ,满足
,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com