
【题目】已知椭圆C的中心在原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点(1, ![]() )在椭圆C上。
)在椭圆C上。
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A,B两点,且△AF2B的面积为![]() ,求以F2为圆心且与直线l相切的圆的方程。
,求以F2为圆心且与直线l相切的圆的方程。
【答案】(1) ![]() (2) (x-1)2+y2=2
(2) (x-1)2+y2=2
【解析】试题分析:(1)设椭圆的方程![]() ,根据定义求得
,根据定义求得![]() 的值,再根据
的值,再根据![]() 的关系,求得
的关系,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)当直线![]() 轴时,求得
轴时,求得![]() ,当直线
,当直线![]() 不垂直
不垂直![]() 轴时,设直线
轴时,设直线![]() 的方程为
的方程为![]() ,联立方程组得到
,联立方程组得到![]() 和
和![]() ,利用弦长公式求得
,利用弦长公式求得![]() 和点到直线的距离公式求解三角形的高(圆的半径),利用三角形的年级得到
和点到直线的距离公式求解三角形的高(圆的半径),利用三角形的年级得到![]() ,进而得到原的方程.
,进而得到原的方程.
试题解析:
(1)设椭圆的方程为![]() =1(a>b>0),由题意可得:
=1(a>b>0),由题意可得:
椭圆C两焦点坐标分别为F1(-1;0),F2(1,0).
所以2a=![]()
所以a=2,又c=1,b2=4-1=3,
故椭圆的方程为![]() .
.
(2)当直线l⊥x轴,计算得到:A(-l,-![]() ),B(-1,
),B(-1, ![]() ),
),
![]() ,不符合题意.
,不符合题意.
当直线l与x轴不垂直时,设直线l的方程为:y=k(x+1),
由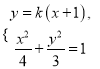 消去y得(3+4k2)x2+8k2x+4k2-12=0,
消去y得(3+4k2)x2+8k2x+4k2-12=0,
显然△>0成立,设A(x1,y1),B(x2,y2),
则x1+x2=![]() ,x1·x2=
,x1·x2=![]() ,
,
又|AB|=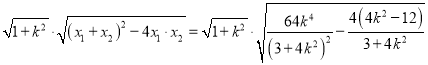 ,
,
即|AB|=![]() ,
,
又圆F2的半径r=![]() ,
,
所以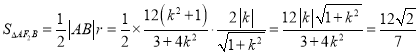 ,
,
化简,得17k4+k2-18=0,
即(k2-1)(17k2+18)=0,解得k=±1,
所以,r=![]() ,故圆F2的方程为:(x-1)2+y2=2.
,故圆F2的方程为:(x-1)2+y2=2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某市为了了解高二学生物理学习情况,在34所高中里选出5所学校,随机抽取了近千名学生参加物理考试,将所得数据整理后,绘制出频率分布直方图如图所示. 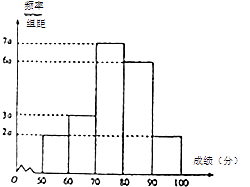
(1)将34所高中随机编号为01,02,…,34,用下面的随机数表选取5组数抽取参加考试的五所学校,选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4所学校的编号是多少?
49 54 43 54 82 17 37 93 23 78 87 35 20
96 43 84 26 34 91 64 57 24 55 06 88 77
04 74 47 67 21 76 33 50 25 83 92 12 06
(2)求频率分布直方图中a的值,试估计全市学生参加物理考试的平均成绩;
(3)如果从参加本次考试的同学中随机选取3名同学,这3名同学中考试成绩在80分以上,(含80分)的人数记为X,求X的分布列及数学期望.(注:频率可以视为相应的概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式|x﹣ ![]() ≤
≤ ![]() 的解集为{x|n≤x≤m}
的解集为{x|n≤x≤m}
(1)求实数m,n;
(2)若实数a,b满足:|a+b|<m,|2a﹣b|<n,求证:|b|< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)的单调函数f(x),对任意的x∈(0,+∞)都有f[f(x)﹣log2x]=6.若x0是方程f(x)﹣f′(x)=4的一个解,且 ![]() ,则a=( )
,则a=( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆相交于
与椭圆相交于![]() ,
, ![]() 两点,
两点, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点,若坐标原点
的中点,若坐标原点![]() 在以
在以![]() 为直径的圆上,求
为直径的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ),若
),若![]() 的一条对称轴离最近的对称中心的距离为
的一条对称轴离最近的对称中心的距离为![]() .
.
(Ⅰ)求![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)在![]() 中角
中角![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 满足
满足![]() 恰是
恰是![]() 的最大值,试判断
的最大值,试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={m|m∈Z,且|m|≤2018},M的子集S满足:对S中任意3个元素a,b,c(不必不同),都有a+b+c≠0.求集合S的元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
(1)求该椭圆的标准方程;
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com