
【题目】如图,已知三棱锥P-ABC中,PA平面ABC,ABAC,且PA=l,AB=AC=2,点D满足![]() ,
,![]() .
.
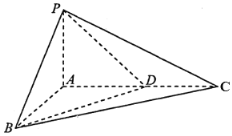
(1)当![]() ,求二面角P-BD-C的余弦值;
,求二面角P-BD-C的余弦值;
(2)若直线PC与平面PBD所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意,以![]() 为正交基底,建立空间直角坐标系A—xyz,求出各点的坐标,进而求出平面的法向量,然后利用空间向量求解二面角的大小;
为正交基底,建立空间直角坐标系A—xyz,求出各点的坐标,进而求出平面的法向量,然后利用空间向量求解二面角的大小;
(2)利用线面角的向量求法可得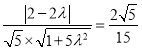 ,解出即可.
,解出即可.
解:(1)∵PA⊥平面ABC,
∴AP⊥AB,AP⊥AC,
又AB⊥AC,
∴以![]() 为正交基底,建立如图所示空间直角坐标系A—xyz,
为正交基底,建立如图所示空间直角坐标系A—xyz,
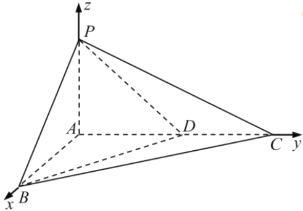
∵PA=1,AB=AC=2,
∴A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,1)
∴![]() ,即D
,即D![]() ,
,
∴![]() ,
,![]() ,
,
设平面PBD的法向量为![]() ,
,
则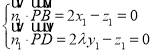 ,取
,取![]() ,
,
当![]() 时,
时,![]() ,又可取
,又可取![]() 为平面BDC的一个法向量,
为平面BDC的一个法向量,
∴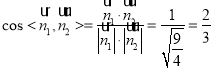 ,
,
由图可知二面角P—BD—C的余弦值为![]() ;
;
(2)![]() ,平面PBD的一个法向量为
,平面PBD的一个法向量为![]() ,
,
设直线PC与平面PBD所成角为![]() ,
,
则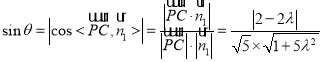 ,
,
结合题设,得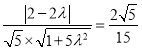 ,即
,即![]() ,
,
解得![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )

A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,点E,F分别为棱BC,CC1的中点,过点A,E,F作平面截正方体的表面所得图形是( )
A.三角形B.平行四边形C.等腰梯形D.平面五边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=2,DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
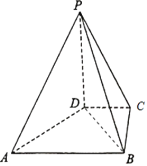
(1)求证:AD⊥PB;
(2)求A点到平面BPC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
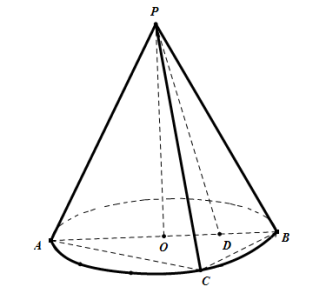
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com