练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（ ）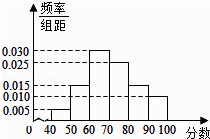
    A.588
    B.480
    C.450
    D.120

    【答案】B
    【解析】解：根据频率分布直方图， 成绩不低于60（分）的频率为1﹣10×（0.005+0.015）=0.8．
    由于该校高一年级共有学生600人，利用样本估计总体的思想，可估计该校高一年级模块测试成绩不低于60（分）的人数为600×0.8=480人．
    故选B．
    根据频率分布直方图，成绩不低于60分的频率，然后根据频数=频率×总数可求出所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数y=ax ， y=xb ， y=logcx的图象如图所示，则a，b，c的大小关系为 ． （用“＜”号连接）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥P﹣ABCD中底面四边形ABCD是正方形，各侧面都是边长为2的正三角形，M是棱PC的中点．建立空间直角坐标系，利用空间向量方法解答以下问题：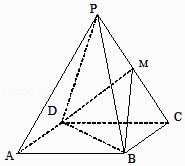
    （1）求证：PA∥平面BMD；
    （2）求二面角M﹣BD﹣C的平面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数 的图象上所有点向左平行移动 个单位长度，得到函数g（x）的图象，则g（x）图象的一条对称轴的方程是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x），定义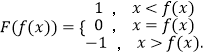
    （Ⅰ）写出函数F（2x﹣1）的解析式；
    （Ⅱ）若F（|x﹣a|）+F（2x﹣1）=0，求实数a的值；
    （Ⅲ）当 时，求h（x）=cosxF（x+sinx）的零点个数和值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 的内角 的对边分别为 ，已知 ．
    （Ⅰ）求角 的大小；
    （Ⅱ）若 ，求 的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体ABCD﹣A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上． （Ⅰ）求异面直线D1E与A1D所成的角；
    （Ⅱ）若二面角D1﹣EC﹣D的大小为45°，求点B到平面D1EC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b∈R，若a2+b2﹣ab=1，则ab的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线l的参数方程为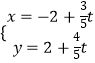： （t为参数），它与曲线C：（y﹣2）2﹣x2=1交于A，B两点．
    （1）求|AB|的长；
    （2）在以O为极点，x轴的正半轴为极轴建立极坐标系，设点P的极坐标为 ，求点P到线段AB中点M的距离．

    查看答案和解析>>

    同步练习册答案