
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() .
.
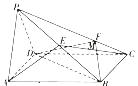
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,要证
,要证![]() 平面
平面![]() ,转证
,转证![]() 即可;
即可;
(2)取![]() 的中点
的中点![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() 利用公式即可得到二面角
利用公式即可得到二面角![]() 的余弦值.
的余弦值.
试题解析:
(Ⅰ)证明:如图5,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵平面![]()
![]() 平面
平面![]() 且
且![]() 为矩形,
为矩形,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
则在直角三角形![]() 中,
中,![]() .
.
又∵![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,则
,则![]() 为
为![]() 的中点,
的中点,
在三角形![]() 中,
中,![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
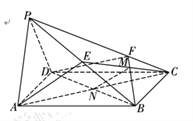
(Ⅱ)解:取![]() 的中点
的中点![]() 为坐标原点,建立如图6所示的空间直角坐标系
为坐标原点,建立如图6所示的空间直角坐标系![]() .
.
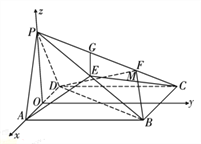
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,
在![]() 中,
中,![]() 为
为![]() 的中点,则
的中点,则![]() 为
为![]() 的中点, 故
的中点, 故![]() .
.
![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]()
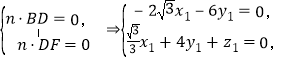 ,
,
解得![]()
平面![]() 的法向量为
的法向量为![]()
设二面角![]() 的平面角为
的平面角为![]()
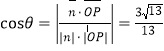 ,因为
,因为![]() 为锐角,
为锐角,
所以二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于![]() 厘米的玉米为高茎玉米,否则为矮茎玉米
厘米的玉米为高茎玉米,否则为矮茎玉米

(1)完成![]() 列联表,并判断是否可以在犯错误概率不超过
列联表,并判断是否可以在犯错误概率不超过![]() 的前提下,认为抗倒伏与玉米矮茎有关?
的前提下,认为抗倒伏与玉米矮茎有关?
(2)为了改良玉米品种,现采用分层抽样的方式从抗倒伏的玉米中抽出![]() 株,再从这
株,再从这![]() 株玉米中选取
株玉米中选取![]() 株进行杂交实验,选取的植株均为矮茎的概率是多少?
株进行杂交实验,选取的植株均为矮茎的概率是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扬州大学数学系有6名大学生要去甲、乙两所中学实习,每名大学生都被随机分配到两所中学的其中一所.
(1)求6名大学生中至少有1名被分配到甲学校实习的概率;
(2)设![]() ,
,![]() 分别表示分配到甲、乙两所中学的大学生人数,记
分别表示分配到甲、乙两所中学的大学生人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学随机选取了![]() 名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图,观察图中数据,完成下列问题.
名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图,观察图中数据,完成下列问题.

(![]() )求
)求![]() 的值及样本中男生身高在
的值及样本中男生身高在![]() (单位:
(单位:![]() )的人数.
)的人数.
(![]() )假设用一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高.
)假设用一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高.
(![]() )在样本中,从身高在
)在样本中,从身高在![]() 和
和![]() (单位:
(单位:![]() )内的男生中任选两人,求这两人的身高都不低于
)内的男生中任选两人,求这两人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校的特长班有![]() 名学生,其中有体育生
名学生,其中有体育生![]() 名,艺术生
名,艺术生![]() 名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于
名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于![]() 次/分到
次/分到![]() 次/分之间.现将数据分成五组,第一组
次/分之间.现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五章
,…,第五章![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
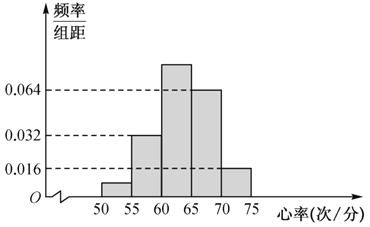
(1)求![]() 的值,并求这
的值,并求这![]() 名同学心率的平均值;
名同学心率的平均值;
(2)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为![]() ,请将下面的列联表补充完整,并判断是否有
,请将下面的列联表补充完整,并判断是否有![]() 的把握认为心率小于
的把握认为心率小于![]() 次/分与常年进行系统的身体锻炼有关?说明你的理由.
次/分与常年进行系统的身体锻炼有关?说明你的理由.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 与圆
与圆![]() 外切于原点
外切于原点![]() ,且两圆圆心的距离
,且两圆圆心的距离![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)过点![]() 的直线
的直线![]() 与圆
与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() ,与圆
,与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com