
【题目】某公司新研发了一款手机应用APP,投入市场三个月后,公司对部分用户做了调研:抽取了400位使用者,每人填写一份综合评分表(满分为100分).现从400份评分表中,随机抽取40份(其中男、女使用者的评分表各20份)作为样本,经统计得到如下的茎叶图:
女性使用者评分 | 男性使用者评分 | |
7 | 6 | 7 8 9 9 |
1 2 5 | 7 | 0 2 2 3 4 5 6 6 7 8 9 |
0 3 3 3 4 4 5 6 6 8 | 8 | 2 4 4 9 |
0 0 1 2 2 2 | 9 | 2 |
记该样本的中位数为![]() ,按评分情况将使用者对该APP的态度分为三种类型:评分不小于
,按评分情况将使用者对该APP的态度分为三种类型:评分不小于![]() 的称为“满意型”,评分不大于
的称为“满意型”,评分不大于![]() 的称为“不满意型”,其余的都称为“须改进型”.
的称为“不满意型”,其余的都称为“须改进型”.
(1)求![]() 的值,并估计这400名使用者中“须改进型”使用者的个数;
的值,并估计这400名使用者中“须改进型”使用者的个数;
(2)为了改进服务,公司对“不满意型”使用者进行了回访,根据回访意见改进后,再从“不满意型”使用者中随机抽取3人进行第二次调查,记这3人中的女性使用者人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
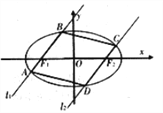
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为两个随机事件,给出以下命题:(1)若
为两个随机事件,给出以下命题:(1)若![]() 为互斥事件,且
为互斥事件,且![]() ,
,![]() ,则
,则![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(3)若
为相互独立事件;(3)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(4)若
为相互独立事件;(4)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(5)若
为相互独立事件;(5)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;其中正确命题的个数为( )
为相互独立事件;其中正确命题的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B两点的坐标分别为(﹣1,0),(1,0).条件甲:A、B、C三点构成以∠C为钝角的三角形;条件乙:点C的坐标是方程x2+2y2=1(y≠0)的解,则甲是乙的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分又不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com