
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且cos2 ![]() =
= ![]() ,△ABC的面积为4.
,△ABC的面积为4.
(1)求 ![]() 的值;
的值;
(2)若2sinB=5sinC,求a的值.
【答案】
(1)解:在△ABC中,∵cos2 ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() ,
,
∴ ![]() ,解得cosA=
,解得cosA= ![]() ,A∈(0,π),
,A∈(0,π),
∴sinA= ![]() =
= ![]() .
.
∵S△ABC=4= ![]() bcsinA=
bcsinA= ![]() bc×
bc× ![]() ,可得bc=10.
,可得bc=10.
![]() =bccosA=10×
=bccosA=10× ![]() =6.
=6.
(2)解:由2sinB=5sinC,得2b=5c,又bc=10,解得b=5,c=2.
∴a2=b2+c2﹣2bccosA=17,
∴a= ![]() .
.
【解析】(1)由cos2 ![]() =
= ![]() ,可得
,可得 ![]() =
= ![]() ,化为cosA=
,化为cosA= ![]() ,A∈(0,π),利用sinA=
,A∈(0,π),利用sinA= ![]() 即可得出.利用S△ABC=4=
即可得出.利用S△ABC=4= ![]() bcsinA,可得bc.即可得出
bcsinA,可得bc.即可得出 ![]() .(2)由2sinB=5sinC,得2b=5c,又bc=10,解得b,c.再利用余弦定理即可得出.
.(2)由2sinB=5sinC,得2b=5c,又bc=10,解得b,c.再利用余弦定理即可得出.
【考点精析】利用余弦定理的定义对题目进行判断即可得到答案,需要熟知余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,圆内接四边形ABCD中,BD是圆的直径,AB=AC,延长AD与BC的延长线相交于点E,作EF⊥BD于F. 
(1)证明:EC=EF;
(2)如果DC= ![]() BD=3,试求DE的长.
BD=3,试求DE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数对(x,y),设映射f:(x,y)→( ![]() ,
, ![]() ),并定义|(x,y)|=
),并定义|(x,y)|= ![]() ,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )
,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )
A.4 ![]()
B.8 ![]()
C.16 ![]()
D.32 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
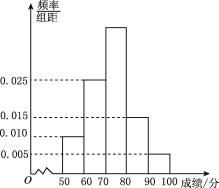
【题目】从2013年开始,国家教育部要求高中阶段每学年都要组织学生进行学生体质健康测试,方案要求以学校为单位组织实施,某校对高一(1)班学生根据《国家学生体质健康标准》的测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图.所示,已知[90,100]分数段的人数为2.
(1)求[70,80)分数段的人数;
(2)现根据预备测试成绩从成绩在80分以上(含80分)的学生中任意选出2人代表班级参加学校举行的一项体育比赛,求这2人的成绩一个在[80,90)分数段、一个在[90,100]分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(3)若函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() .设
.设![]() ,其中常数
,其中常数![]() 、
、![]() 满足条件
满足条件![]() ,且
,且![]() .试判断在点
.试判断在点![]() 处的切线斜率的正负,并说明理由.
处的切线斜率的正负,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)记F(x)=f(x)﹣g(x),判断F(x)在区间(1,2)内零点个数并说明理由;
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并给出对应的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com