
设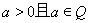 ,
,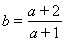 .
.
(Ⅰ)证明: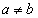 ;
;
(Ⅱ)求证:在数轴上,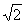 介于
介于 与
与 之间,且距
之间,且距 较远;
较远;
(Ⅲ)在数轴上, 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,
说明理由.
略
【解析】
试题分析:i(Ⅰ) 证明不成立问题一般采用反证法,即假设问题成立,从假设开始推理论证得出矛盾,则说明假设不成立原命题成立。(Ⅱ)只需证明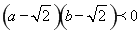 即可说明
即可说明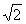 介于
介于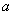 与
与 之间。下面应分两种情况证明,当
之间。下面应分两种情况证明,当 时,用作差法比较
时,用作差法比较 和
和  的大小当
的大小当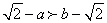 时,说明
时,说明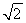 距
距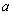 较远。当
较远。当 时同理可证。(Ⅲ)用反证法:假设存在整数m为
时同理可证。(Ⅲ)用反证法:假设存在整数m为 之间的距离,不妨设
之间的距离,不妨设 ,将
,将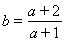 代入上式整理可得关于
代入上式整理可得关于 的一元二次方程。用求根公式可将
的一元二次方程。用求根公式可将 解出。若与已知
解出。若与已知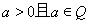 相矛盾,则说明假设不成立,否则假设成立。
相矛盾,则说明假设不成立,否则假设成立。
试题解析:(Ⅰ)假设 与已知
与已知 ,
,
所以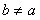 . 3分
. 3分
(Ⅱ)因为 ,所以
,所以
所以 或
或 。即
。即 或
或 。所以
。所以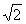 介于
介于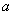 与
与 之间。
之间。
若 则
则 ,
,
因为 ,所以
,所以 ,
,
则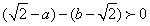 ,所以
,所以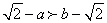 ,所以
,所以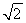 距
距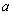 较远。
较远。
当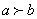 时,同理可证。
时,同理可证。
综上可得在数轴上,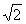 介于
介于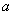 与
与 之间,且距
之间,且距 较远。
较远。
(Ⅲ)假设存在整数m为 之间的距离,不妨设
之间的距离,不妨设 ,
,
则有 ,因为
,因为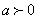 ,所以
,所以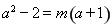 ,即
,即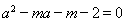 。所以
。所以 。因为
。因为 ,所以只有
,所以只有 。当
。当 时,
时, 或
或 ,与假设
,与假设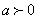 矛盾,故,
矛盾,故, 之间的距离不可能为整数。
之间的距离不可能为整数。
考点:作差法比较大小、反证法。


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
 把函数y=f(x)在x=a及x=b之间的一段图象近似地看作直线,设a≤c≤b,
把函数y=f(x)在x=a及x=b之间的一段图象近似地看作直线,设a≤c≤b,| c-a | b-a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| -3f/(an)+9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| an+2 |
| 1 |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+2 |
| an+1 |
| 7 |
| 5 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an-2n | 3n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com