
定义域为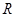 的函数
的函数 ,若函数
,若函数 有
有 个不同的零点
个不同的零点 ,
, ,
, ,
, ,
, ,则
,则 等于_______________
等于_______________
15
解析试题分析:根据已知条件可知,分段函数f(x)的图像,再单独定义一个(1,1)点即可。
整个函数图像是关于x=1对称的,且f(x)>0恒成立。函数 有
有 个不同的零点
个不同的零点 ,
, ,
, ,
, ,
, ,不妨令
,不妨令








因为从总体上来说f(x)是一个关于f(x)的二次函数,即最多只会有2个不同的f(x)解,那么只能是每个f(x)对应了2个不等的与x=1对称的关于x的实根,再加上x=1,一共就有5个了!所以说
因为f(1)=1,则 ,代入点(1,0)到
,代入点(1,0)到 中,有1+b+
中,有1+b+ =0,b=-
=0,b=-
所以f(x)=0,则有 ,当f(x)=1时则有
,当f(x)=1时则有
当f(x)= 时则有
时则有 ,因此可知
,因此可知 =15,故答案为15.
=15,故答案为15.
考点:本试题考查了函数与方程的运用。
点评:解决该试题的关键是理解方程的根与函数f(x)的关系,然后结合分段函数的图像来得到各个交点具有的对称性,进而得到运算的结果,属于难度题。


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:填空题
函数 ,其中
,其中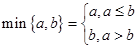 ,若动直线
,若动直线 与函数
与函数 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 ,则
,则 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com