
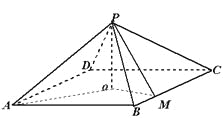
【题目】如图,四棱锥![]() 中,底面是以
中,底面是以![]() 为中心的菱形,
为中心的菱形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0, ![]() ).
).
(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 令Tn= ![]() ,称Tn为数列a1 , a2 , …,an的“理想数”,已知数列a1 , a2 , …,a502的“理想数”为2012,那么数列2,a1 , a2 , …,a502的“理想数”为( )
,称Tn为数列a1 , a2 , …,an的“理想数”,已知数列a1 , a2 , …,a502的“理想数”为2012,那么数列2,a1 , a2 , …,a502的“理想数”为( )
A.2010
B.2011
C.2012
D.2013
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D是△ABC边BC延长线上一点,记 ![]()
![]() .若关于x的方程2sin2x﹣(λ+1)sinx+1=0在[0,2π)上恰有两解,则实数λ的取值范围是( )
.若关于x的方程2sin2x﹣(λ+1)sinx+1=0在[0,2π)上恰有两解,则实数λ的取值范围是( )
A.λ<﹣2
B.λ<﹣4
C.![]()
D.λ<﹣4或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosx,﹣
=(cosx,﹣ ![]() ),
), ![]() =(sinx+cosx,1),f(x)=
=(sinx+cosx,1),f(x)= ![]()
![]() ,
,
(1)若0<α< ![]() ,sinα=
,sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通项公式;
(2)求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com