
【题目】在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,已知a=![]() c.
c.
(1)若∠A=2∠B,求cosB;
(2)若AC=2,求△ABC面积的最大值.
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() (
( ![]() )的右焦点为F,右顶点为A,已知
)的右焦点为F,右顶点为A,已知 ![]() ,其中O 为原点, e为椭圆的离心率.
,其中O 为原点, e为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点A的直线l与椭圆交于点B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若 ![]() ,且
,且 ![]() ,求直线的l斜率.
,求直线的l斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设公差大于0的等差数列{ ![]() }的前n项和为
}的前n项和为 ![]() .已知
.已知 ![]() ,且
,且 ![]() ,
, ![]() ,
, ![]() 成等比数列.记数列
成等比数列.记数列 ![]() 的前n项和为
的前n项和为 ![]() .
.
(1)求 ![]() ;
;
(2)若对于任意的n ![]() ,k
,k ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥P﹣ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA= ![]() ,PB=
,PB= ![]() ,则三棱锥P﹣ABC的外接球的表面积为 .
,则三棱锥P﹣ABC的外接球的表面积为 . 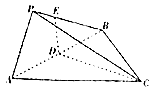
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在30天内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段![]() ,
,![]() (不包含
(不包含![]() ,
,![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.
第 | 5 | 1 5 | 2 0 | 3 0 |
销售量 | 3 5 | 2 5 | 2 0 | 1 0 |
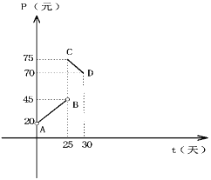
(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的中心在原点,焦点在
的中心在原点,焦点在 ![]() 轴上,长轴长为4,且点
轴上,长轴长为4,且点 ![]() 在椭圆
在椭圆 ![]() 上.
上.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设 ![]() 是椭圆
是椭圆 ![]() 长轴上的一个动点,过
长轴上的一个动点,过 ![]() 作斜率为
作斜率为 ![]() 的直线
的直线 ![]() 交椭圆
交椭圆 ![]() 于
于 ![]() 、
、 ![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一动点 ![]() 到点
到点 ![]() 的距离与点
的距离与点 ![]() 到 x
到 x![]() 轴的距离的差等于1.
轴的距离的差等于1.
(1)求动点 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(2)过点 ![]() 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ![]() ,设
,设 ![]() 与轨迹
与轨迹 ![]() 相交于点
相交于点 ![]() ,
, ![]() 与轨迹
与轨迹 ![]() 相交于点
相交于点 ![]() ,求
,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,
, ![]() 且
且![]() ,则
,则![]() 的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com