

 可得答案;
可得答案;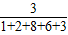 =
= .
. =
= ,解得n=40.…(4分)
,解得n=40.…(4分) ×40=2人,记为x,y;成绩在[80,95)上的学生有
×40=2人,记为x,y;成绩在[80,95)上的学生有 ×40=4人,记为a,b,c,d.
×40=4人,记为a,b,c,d. =
= .…(12分)
.…(12分)

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
 为了解某校高三学生9月调考数学成绩的分布情况,从该校参加考试的学生数学成绩中抽取一个样本,并分成5组,绘制成如图所示的频率分布直方图.已知第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频数为6.
为了解某校高三学生9月调考数学成绩的分布情况,从该校参加考试的学生数学成绩中抽取一个样本,并分成5组,绘制成如图所示的频率分布直方图.已知第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频数为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某校高三学生9月调考数学成绩的分布情况,从该校参加考试的学生数学成绩中抽取一个样本,并分成5组,绘制成如图所示的频率分布直方图.已知第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频数为6.
为了解某校高三学生9月调考数学成绩的分布情况,从该校参加考试的学生数学成绩中抽取一个样本,并分成5组,绘制成如图所示的频率分布直方图.已知第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频数为6.查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉市高三(上)11月调考数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉市高三(上)11月调考数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com