
【题目】三棱柱![]() ,侧棱与底面垂直,
,侧棱与底面垂直, ![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
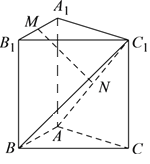
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)欲证![]() 平面
平面![]() ,根据直线与平面平行的判定定理可知只需证
,根据直线与平面平行的判定定理可知只需证![]() 与平面
与平面![]() 内一直线平行即可,而连接
内一直线平行即可,而连接![]() ,根据中位线定理可知
,根据中位线定理可知![]() , 又
, 又![]() 平面
平面![]() 满足定理所需条件;(2)证明
满足定理所需条件;(2)证明![]() ,即可证明
,即可证明![]() 平面
平面![]() ,从而证明平面
,从而证明平面![]() 平面
平面![]() .
.
试题解析:(1)连接![]() .在
.在![]() 中,∵
中,∵![]() ,
, ![]() 是
是![]() ,
, ![]() 的中点,
的中点,
∴![]()
![]() ,又∵
,又∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(![]() )∵三棱柱
)∵三棱柱![]() 中,侧棱与底面垂直,∴四边形
中,侧棱与底面垂直,∴四边形![]() 是正方形,∴
是正方形,∴![]() ,
,
∴![]() ,连接
,连接![]() ,
, ![]() ,则
,则![]() ≌
≌![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、平面与平面垂直的判定定理,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 ![]() ,
, ![]()
(1)分别求出小球落入A袋和B袋中的概率;
(2)在容器 入口处依次放入4个小球,记ξ为落入B袋中的小球个数,求ξ的分布列和数学期望.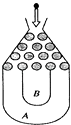
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com