Question

【题目】如图，在四边形ABCD中，AB=BC=2，∠ABC=90°，DA=DC= ．现沿对角线AC折起，使得平面DAC⊥平面ABC，此时点A，B，C，D在同一个球面上，则该球的体积是（ ）
A.
B.
C.
D.12π

Answer 1

【答案】A
【解析】解：在图2中，取AC的中点E，连结DE，BE， ∵AD=CD，∴DE⊥AC，
∵平面ACD∩平面ABC=AC，平面ACD⊥平面ABC，
DE平面ACD，
∴DE⊥平面ABC，
∵∠ABC=90°，
∴棱锥外接球的球心O在直线DE上，
∵AD=CD= ，AB=BC=2，∠ABC=90°，
∴BE=AE=CE= AC= ，DE= =2，
设OE=x，则OD=2﹣x，OB= = ，
∴2﹣x= ，解得x= ，
∴外接球的半径r=2﹣x= ，
∴外接球的体积V= = ×（ ）3= ．
故选A．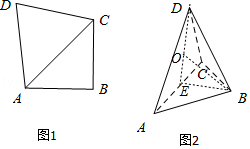

【考点精析】解答此题的关键在于理解球内接多面体的相关知识，掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．