
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点
.不过原点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,且线段
两点,且线段![]() 被直线
被直线![]() 平分.
平分.
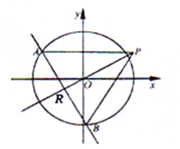
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的面积取最大值时直线
的面积取最大值时直线![]() 的方程.
的方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本,(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出如下频率分布直方图.
的分组作出如下频率分布直方图.
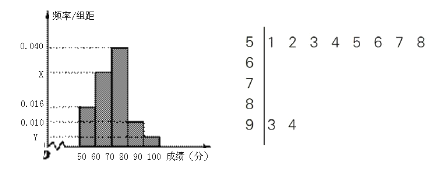
(1)由如下茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据)提供的信息,求样本容量
的数据)提供的信息,求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,求所抽取的2名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的极值;
的极值;
(Ⅱ)设函数![]() .当
.当![]() 时,若区间
时,若区间![]() 上存在
上存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体户计划经销A、B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A、B商品中所获得的收益分别为f(x)万元与g(x)万元、其中f(x)=a(x﹣1)+2(a>0);g(x)=6ln(x+b),(b>0)已知投资额为零时,收益为零.
(1)试求出a、b的值;
(2)如果该个体户准备投入5万元经营这两种商品,请你帮他制定一个资金投入方案,使他能获得最大收益,并求出其收入的最大值.(精确到0.1,参考数据:ln3≈1.10).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0).
(1)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(2)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,锐角△ABC中, ![]() =
= ![]() ,
, ![]() =
= ![]() ,点M为BC的中点. (Ⅰ)试用
,点M为BC的中点. (Ⅰ)试用 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(Ⅱ)若| ![]() |=5,|
|=5,| ![]() |=3,sin∠BAC=
|=3,sin∠BAC= ![]() ,求中线AM的长.
,求中线AM的长.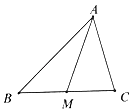
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com