




 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, ,
, (
( 为虚数单位)的正四面体玩具连续抛掷两次,第一次出现底面朝下的复数记为
为虚数单位)的正四面体玩具连续抛掷两次,第一次出现底面朝下的复数记为 ,第二次出现底面朝下的复数记为
,第二次出现底面朝下的复数记为 .
. 表示“
表示“ ”这一事件,求事件
”这一事件,求事件 的概率
的概率 ;
; 的实部为
的实部为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.只与k有关 | B.只与μ有关 |
| C.只与σ有关 | D.只与μ和σ有关 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 围棋社 | 舞蹈社 | 拳击社 | |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、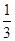 、
、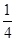 ,记该参加者闯三关所得总分为ξ.
,记该参加者闯三关所得总分为ξ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com