
【题目】已知![]() AOB的一个顶点O是抛物线C:
AOB的一个顶点O是抛物线C:![]() 的顶点,A、B两点都在C上,且
的顶点,A、B两点都在C上,且![]() =0,
=0,
(1)证明:直线AB恒过定点P(2,0)
(2)求![]() AOB面积的最小值
AOB面积的最小值
【答案】(1)证明过程见详解;(2)4.
【解析】
(1)由![]() 得
得![]() 所在直线与
所在直线与![]() 所在的直线垂直,设出直线方程,与抛物线方程联立求出
所在的直线垂直,设出直线方程,与抛物线方程联立求出![]() 、
、![]() 两点的坐标,由两点式得直线AB的方程,化简整理即可得到答案.
两点的坐标,由两点式得直线AB的方程,化简整理即可得到答案.
(2)由(1)的结论设出直线AB的方程,联立直线与抛物线的方程化简,由根与系数的关系及弦长公式即可求得![]() 的面积的表达式,利用二次函数的性质即可得到答案.
的面积的表达式,利用二次函数的性质即可得到答案.
(1)依题设![]() 所在的直线为
所在的直线为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 所在的直线为
所在的直线为![]() ,
,
由![]() 解得
解得![]() 或
或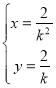 ,
,
所以![]() 点的坐标为
点的坐标为![]() .
.
同理由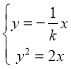 可得
可得![]() 点的坐标为
点的坐标为![]()
所以![]() 所在的直线方程为
所在的直线方程为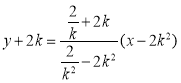 ,
,
化简整理得:![]() ,
,
所以对任何不为0的实数![]() ,当
,当![]() 时,恒有
时,恒有![]() ,
,
所以直线AB恒过定点![]() .
.
(2)由(1)知直线AB恒过定点![]() ,
,
则可直线AB的方程为![]() ,设
,设![]()
由![]() 得
得![]() ,
,
则![]()
所以![]()
![]() ,
,
所以![]()
![]()
![]()
所以当![]() 时,
时,![]() 的面积取得最小值为
的面积取得最小值为![]()


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,四分位数是指把一组数由小到大排列并分成四等份,处于三个分割点位置的数值为![]() ,
,![]() ,
,![]() ,其中
,其中![]() 是这组数的中位数,
是这组数的中位数,![]() 和
和![]() 分别可看作这组数被
分别可看作这组数被![]() 分成的前后两组数的中位数.利用四分位数可以绘制统计学中的箱形图:先找出一组数的最大值、最小值和三个四分位数
分成的前后两组数的中位数.利用四分位数可以绘制统计学中的箱形图:先找出一组数的最大值、最小值和三个四分位数![]() ;然后连接
;然后连接![]() 和
和![]() 画出“箱子”,中位数
画出“箱子”,中位数![]() 在“箱子”中间;再将最大值和最小值与箱子相连接(如图①).某老师绘制了一次数学小测验中甲、乙、丙三个班级学生得分的箱形图(如图②),根据该图判断下列说法错误的是( )
在“箱子”中间;再将最大值和最小值与箱子相连接(如图①).某老师绘制了一次数学小测验中甲、乙、丙三个班级学生得分的箱形图(如图②),根据该图判断下列说法错误的是( )
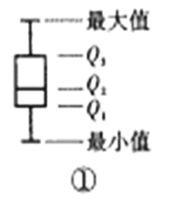
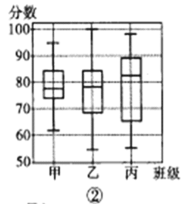
A.三个班级中,甲班分数的方差最小
B.三个班级中,乙班分数的极差最大
C.丙班得分低于80的学生人数多于得分高于80的学生人数
D.若每班有42个学生,则三个班级的第11名中,丙班的分数最高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在![]() 之间,其得分的频率分布直方图如图,则下列结论错误的是( )
之间,其得分的频率分布直方图如图,则下列结论错误的是( )
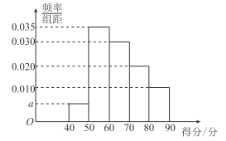
A.得分在![]() 之间的共有40人
之间的共有40人
B.从这100名参赛者中随机选取1人,其得分在![]() 的概率为0.5
的概率为0.5
C.估计得分的众数为55
D.这100名参赛者得分的中位数为65
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对于函数f(x)定义域内任意的两个自变量的值x1,x2,当x1<x2时,都有f(x1)≤f(x2),且存在两个不相等的自变量值y1,y2,使得f(y1)=f(y2),就称f(x)为定义域上的不严格的增函数.则①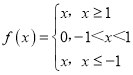 ,②
,②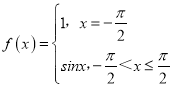 ,③
,③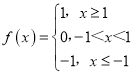 ,④
,④![]() ,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在![]() 米以上的进入决赛,把所得的成绩进行整理后,分成
米以上的进入决赛,把所得的成绩进行整理后,分成![]() 组画出频率分布直方图的一部分(如图),已知第
组画出频率分布直方图的一部分(如图),已知第![]() 组的频数是
组的频数是![]() .
.
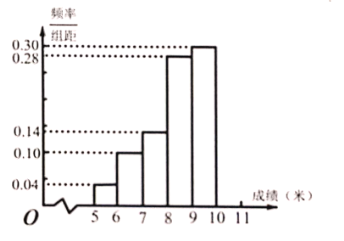
(1)求进入决赛的人数;
(2)用样本的频率代替概率,记![]() 表示两人中进入决赛的人数,求
表示两人中进入决赛的人数,求![]() 得分布列及数学期望.
得分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com