
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ) 求曲线![]() 与
与![]() 交点的平面直角坐标;
交点的平面直角坐标;
(Ⅱ) 点![]() 分别在曲线
分别在曲线![]() ,
, ![]() 上,当
上,当![]() 最大时,求
最大时,求![]() 的面积(
的面积(![]() 为坐标原点).
为坐标原点).
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】定义:在等式![]()
![]()
![]()
![]() 中,把
中,把![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 叫做三项式的
叫做三项式的![]() 次系数列(如三项式的1次系数列是1,1,1).
次系数列(如三项式的1次系数列是1,1,1).
(1)填空:三项式的2次系数列是_______________;
三项式的3次系数列是_______________;
(2)由杨辉三角数阵表可以得到二项式系数的性质![]() ,类似的请用三项式
,类似的请用三项式![]() 次系数列中的系数表示
次系数列中的系数表示![]() (无须证明);
(无须证明);
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为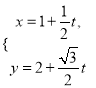 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆:
中,椭圆: ![]() 的离心率为
的离心率为![]() ,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 已知椭圆的上顶点为A,点B,C是上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() .
.
① 求证: ![]() 为定值;
为定值;
② 求△CEF的面积的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
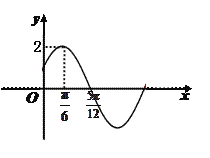
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-1|+|2x-1|.
(Ⅰ)若对![]() x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
(Ⅱ)在(Ⅰ)成立的条件下,正实数a,b满足a2+b2=2M.证明:a+b≥2ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
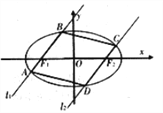
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com