
【题目】在用二分法求方程![]() 在区间
在区间![]() 内的近似解时,先将方程变形为
内的近似解时,先将方程变形为![]() ,构建
,构建![]()
![]() ,然后通过计算以判断
,然后通过计算以判断![]() 及
及![]() 的正负号,再按步骤取区间中点值,计算中点的函数近似值,如此往复缩小零点所在区间,计算得部分数据列表如下:
的正负号,再按步骤取区间中点值,计算中点的函数近似值,如此往复缩小零点所在区间,计算得部分数据列表如下:
步骤 | 区间左端点 | 区间右端点 |
| 中点 |
1 | 2 | 3 | 2.5 | -0.102 |
2 | 0.189 | |||
3 | 2.625 | 0.044 | ||
4 | 2.5 | 2.625 | 2.5625 | -0.029 |
5 | 2.5625 | 2.625 | 2.59375 | 0.008 |
6 | 2.5625 | 2.59375 | 2.578125 | -0.011 |
7 | 2.578125 | 2.59375 | 2.5859375 | -0.001 |
8 | 2.5859375 | 2.59375 | 2.58984375 | 0.003 |
9 | 2.5859375 | 2.58984375 | 2.587890625 | 0.001 |
(1)判断![]() 及
及![]() 的正负号;
的正负号;
(2)请完成上述表格,在空白处填上正确的数字;
(3)若给定的精确度为0.1,则到第几步骤即可求出近似值?此时近似值为多少?
(4)若给定的精确度为0.01,则需要到第几步骤才可求出近似值?近似值为多少?
【答案】(1)![]() (2)见解析;(3)第5步骤;2.625;(4)第8步骤;
(2)见解析;(3)第5步骤;2.625;(4)第8步骤;![]()
【解析】
(1)利用![]() 的解析式求出
的解析式求出![]() ,
,![]() 判断与0的大小关系即可;
判断与0的大小关系即可;
(2)由于![]() ,故零点在
,故零点在![]() 之间,故步骤2的左端点和右端点分别为2.5,3,中点的值为
之间,故步骤2的左端点和右端点分别为2.5,3,中点的值为![]() ,同理可得到步骤3的值;
,同理可得到步骤3的值;
(3)使得左端点和右端点差的绝对值小于0.1即可,由表可知,到步骤5满足条件.
(4) 使得左端点和右端点差的绝对值小于0.01即可,由表可知,到步骤8满足条件.
解:(1)![]()
![]() ,
,![]()
![]()
(2)如下表;
步骤 | 区间左端点 | 区间右端点 |
| 中点 |
1 | 2 | 3 | 2.5 | -0.102 |
2 | 2.5 | 3 | 2.75 | 0.189 |
3 | 2.5 | 2.75 | 2.625 | 0.044 |
4 | 2.5 | 2.625 | 2.5625 | -0.029 |
5 | 2.5625 | 2.625 | 2.59375 | 0.008 |
6 | 2.5625 | 2.59375 | 2.578125 | -0.011 |
7 | 2.578125 | 2.59375 | 2.5859375 | -0.001 |
8 | 2.5859375 | 2.59375 | 2.58984375 | 0.003 |
9 | 2.5859375 | 2.58984375 | 2.587890625 | 0.001 |
(3)直到第5步骤时,考虑到![]() ,此时可求出零点的近似值为
,此时可求出零点的近似值为![]() .(可取区间
.(可取区间![]() 内任意值)
内任意值)
(4)直到第8步骤时,考虑到![]() ,此时可求出零点的近似值为
,此时可求出零点的近似值为![]() .(可取
.(可取![]() 内任意值)
内任意值)


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 满足(1)对于定义域上的任意
满足(1)对于定义域上的任意![]() ,恒有
,恒有![]() ;(2)对于定义域上的任意
;(2)对于定义域上的任意![]() 当
当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”,给出下列四个函数中:①
为“理想函数”,给出下列四个函数中:① ![]() ; ②
; ②![]() ;③
;③![]() ;④
;④ ,则被称为“理想函数”的有( )
,则被称为“理想函数”的有( )
A.①B.②④C.③D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左焦点与抛物线
,其左焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)过动点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() 在第一象限,
在第一象限,![]() ,过点
,过点![]() 做
做![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() ,连接
,连接![]() 并延长交椭圆
并延长交椭圆![]() 于另一点
于另一点![]() .设直线
.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值.
为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
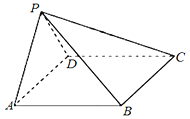
(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-a-lnx,其中a ∈R.
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com