
【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC. 
(1)若∠DAC=30°,求角B的大小;
(2)若BD=2DC,且AD=3 ![]() ,求DC的长.
,求DC的长.
【答案】
(1)解:在△ABC中,由正弦定理得: ![]() =
= ![]() ,
,
由题意得:sin∠ADC= ![]() sin∠DAC=
sin∠DAC= ![]() ,
,
∵∠ADC=∠B+∠BAD=∠B+60°>60°,
∴∠ADC=120°,
∴∠B=60°
(2)解:设DC=x,则BD=2x,BC=3x,AC= ![]() x,
x,
在Rt△ABC中,sinB= ![]() =
= ![]() ,AB=
,AB= ![]() x,
x,
∴cosB= ![]() ,
,
在△ABD中,由余弦定理得:(3 ![]() )2=6x2+4x2﹣2×
)2=6x2+4x2﹣2× ![]() x×2x×
x×2x× ![]() ,
,
解得:x=3,
则DC=3
【解析】(1)利用正弦定理求出sin∠ADC的值,进而求出∠ADC的度数,即可求出∠B的度数;(2)设DC=x,表示出BD,BC,以及AC,利用同角三角函数间的基本关系及余弦定理求出x的值,确定出DC的长即可.


科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如表:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(Ⅰ)试分别估计芯片甲,芯片乙为合格品的概率;
(Ⅱ)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2. 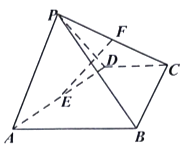
(Ⅰ)证明:直线EF∥平面PAB;
(Ⅱ)求直线EF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( ) 
A.4
B.5
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣2|x+1|.
(1)求f(x)的最大值;
(2)若存在x∈[﹣2,1]使不等式a+1>f(x)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车进驻城市,绿色出行引领时尚,某市有统计数据显示,2016年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示,若将共享单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”,已知在“经常使用单车用户”中有 ![]() 是“年轻人”.
是“年轻人”. 
(Ⅰ)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列2×2列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?
使用共享单车情况与年龄列联表
年轻人 | 非年轻人 | 合计 | |
经常使用共享单车用户 | 120 | ||
不常使用共享单车用户 | 80 | ||
合计 | 160 | 40 | 200 |
(Ⅱ)将频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量X,求X的分布列与期望.
(参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中,K2= ![]() ,n=a+b+c+d)
,n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为  ,曲线C的极坐标方程为
,曲线C的极坐标方程为 ![]()
(1)求曲线C的直角坐标方程;
(2)设直线A与曲线C相交于A,B两点,已知定点P( ![]() ,0),当α=
,0),当α= ![]() 时,求|PA|+|PB|的值.
时,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的焦点和上顶点分别为F1、F2、B,定义:△F1BF2为椭圆C的“特征三角形”,如果两个椭圆的特征三角形是相似三角形,那么称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比,已知点
的焦点和上顶点分别为F1、F2、B,定义:△F1BF2为椭圆C的“特征三角形”,如果两个椭圆的特征三角形是相似三角形,那么称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比,已知点 ![]() 是椭圆
是椭圆 ![]() 的一个焦点,且C1上任意一点到它的两焦点的距离之和为4.
的一个焦点,且C1上任意一点到它的两焦点的距离之和为4.
(1)若椭圆C2与椭圆C1相似,且C2与C1的相似比为2:1,求椭圆C2的方程;
(2)已知点P(m,n)(mn≠0)是椭圆C1上的任意一点,若点Q是直线y=nx与抛物线 ![]() 异于原点的交点,证明:点Q一定在双曲线4x2﹣4y2=1上;
异于原点的交点,证明:点Q一定在双曲线4x2﹣4y2=1上;
(3)已知直线l:y=x+1,与椭圆C1相似且短半轴长为b的椭圆为Cb , 是否存在正方形ABCD,(设其面积为S),使得A、C在直线l上,B、D在曲线Cb上?若存在,求出函数S=f(b)的解析式及定义域;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com