
【题目】水葫芦原产于巴西,![]() 年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过
年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() ,经过
,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() . 现水葫芦覆盖面积
. 现水葫芦覆盖面积![]() (单位
(单位![]() )与经过时间
)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(参考数据:![]() )
)
(Ⅰ)试判断哪个函数模型更合适,并求出该模型的解析式;
(Ⅱ)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的![]() 倍.
倍.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,经过点
,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)记![]() 与
与![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 关于
关于![]() 的表达式,并求出当
的表达式,并求出当![]() 为何值时
为何值时![]() 有最大值.
有最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人做定点投篮游戏,已知甲每次投篮命中的概率均为![]() ,甲投篮3次均未命中的概率为
,甲投篮3次均未命中的概率为![]() ,乙每次投篮命中的概率均为
,乙每次投篮命中的概率均为![]() ,乙投篮2次恰好命中1次的概率为
,乙投篮2次恰好命中1次的概率为![]() ,甲、乙每次投篮是否命中相互之间没有影响.
,甲、乙每次投篮是否命中相互之间没有影响.
(1)若乙投篮3次,求至少命中2次的概率;
(2)若甲、乙各投篮2次,设两人命中的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥A-BCDE中,底面BCDE为直角梯形,CD⊥平面ABC,侧面ABCD是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE,点M是棱AD的中点
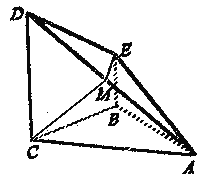
(1)求异面直线ME与AB所成角的大小;
(Ⅱ)证明:平面AED⊥平面ACD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (φ为参数,0≤φ≤π),曲线C2的参数方程为
(φ为参数,0≤φ≤π),曲线C2的参数方程为  (t为参数).
(t为参数).
(1)求C1的普通方程并指出它的轨迹;
(2)以O为极点,x轴的非负半轴为极轴建立极坐标系,射线OM:θ= ![]() 与半圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与半圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点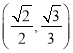 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点作斜率为
的右顶点作斜率为![]() (
(![]() )的直线交椭圆
)的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线a、b和平面![]() ,下列说法中正确的有______ .
,下列说法中正确的有______ .
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若直线
若直线![]() ,直线
,直线![]() ,则
,则![]() ;
;
![]() 若直线a在平面
若直线a在平面![]() 外,则
外,则![]() ;
;
![]() 直线a平行于平面
直线a平行于平面![]() 内的无数条直线,则
内的无数条直线,则![]() ;
;
![]() 若直线
若直线![]() ,那么直线a就平行于平面
,那么直线a就平行于平面![]() 内的无数条直线.
内的无数条直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C的极坐标方程为ρ=6cosθ+2sinθ,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设点Q(1,2),直线l与曲线C交于A,B两点,求|QA||QB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 表示两个不同的平面,
表示两个不同的平面, ![]() 表示两条不同直线,对于下列两个命题:
表示两条不同直线,对于下列两个命题:
①若![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②若![]() ,则“
,则“![]() ”是“
”是“![]() 且
且![]() ”的充要条件.判读正确的是( )
”的充要条件.判读正确的是( )
A. ①②都是真命题 B. ①是真命题,②是假命题
C. ①是假命题,②是真命题 D. ①②都是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com