
【题目】已知椭圆与抛物线y2=![]() x有一个相同的焦点,且该椭圆的离心率为
x有一个相同的焦点,且该椭圆的离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过点P(0,1)的直线与该椭圆交于A,B两点,O为坐标原点,若![]() ,求△AOB的面积.
,求△AOB的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)先求椭圆焦点得c,再根据离心率列方程组可得a=2,b2=2 (2)将OP视为底,根据三角形面积公式得S=![]() |OP|·|x1-x2|,再联立直线方程与椭圆方程,利用韦达定理化简得|x1-x2|,最后根据
|OP|·|x1-x2|,再联立直线方程与椭圆方程,利用韦达定理化简得|x1-x2|,最后根据![]() 解出k,代入解得△AOB的面积.
解出k,代入解得△AOB的面积.
试题解析:解:(1)依题意,设椭圆的标准方程为![]() +
+![]() =1(a>b>0),
=1(a>b>0),
由题意可得c=![]() ,又e=
,又e=![]() =
=![]() ,∴a=2.
,∴a=2.
∴b2=a2-c2=2,
∴椭圆的标准方程为![]() +
+![]() =1.
=1.
(2)设A(x1,y1),B(x2,y2),
由![]() =2
=2![]() ,得
,得![]()
设直线AB的方程为y=kx+1,代入椭圆方程整理,得
(2k2+1)x2+4kx-2=0,
∴x1+x2=-![]() ,x1·x2=-
,x1·x2=-![]() .
.
将x1=-2x2代入上式整理可得,![]() 2=
2=![]() ,
,
解得k2=![]() .
.
∴△AOB的面积S=![]() |OP|·|x1-x2|
|OP|·|x1-x2|
=![]() =
=![]() ·
·![]() =
=![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.8元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.

(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
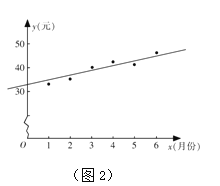
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}(n∈N*),首项a1=3,前n项和为Sn,且S3+a3、S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)数列{nan}的前n项和为Tn,若对任意正整数n,都有Tn∈[a,b],求b-a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通项公式;
(2)若T3=21,求S3.
查看答案和解析>>
科目:高中数学 来源: 题型:
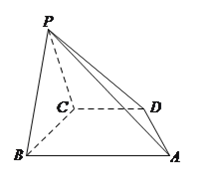
【题目】在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小.
)的大小.
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2![]() ,AB=1,AC=2,∠BAC=60°,则球O的表面积为
,AB=1,AC=2,∠BAC=60°,则球O的表面积为
A. 4![]() B. 12
B. 12![]() C. 16
C. 16![]() D. 64
D. 64![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
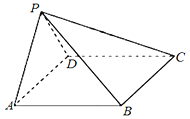
(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立极坐标系,曲线
轴的正半轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
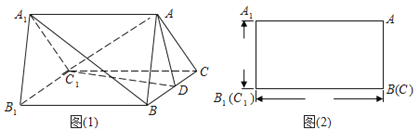
【题目】如图(1)是一个水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中点.正三棱柱的正(主)视图如图(2).
的中点.正三棱柱的正(主)视图如图(2).
(Ⅰ)求正三棱柱![]() 的体积;
的体积;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)图(1)中垂直于平面![]() 的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com