
【题目】如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,![]() .
.
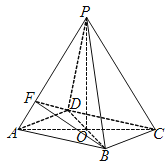
(1)求四棱锥P-ABCD的体积VP-ABCD;
(2)在线段PB上是否存在一点M,使得CM∥平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
【答案】(1)2;(2)![]()
【解析】
(1)证明PO⊥平面ABCD,计算PO,AC,BD,代入体积公式计算;
(2)过C构造平面BCE,使得平面BCE∥BDF,利用三角形的中线的性质得出M的位置.
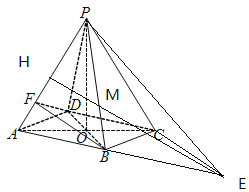
(1)解:∵底面ABCD是菱形,∴O为AC,BD的中点
又∵PA=PC,PB=PD,∴PO⊥AC,PO⊥BD,
∵AC∩BD=O,AC面ABCD,BD面ABCD,
∴PO⊥底面ABCD.
△PAC中,AC=2,∴![]() ,△PBD中,
,△PBD中,![]() ,
,![]() ,
,
![]() .
.
(2)过C作CE∥BD交AB延长线于E,过E作EH∥BF交PA于H,EH与PB交点为M,
∵CE∥BD,BD面BDF,CE面BDF,∴CE∥面BDF,
∵EH∥BF,BF面BDF,EH面BDF,∴EH∥面BDF,
又∵CE∩EH=E,CE面CEM,EH面CEM,
∴面BDF∥面CEM,CM面CEM,
∴CM∥面BDF,
∵BD∥CE,DC∥BE,
∴四边形BECD为平行四边形,∴DC=BE=AB,B为AE中点,
∵![]() ∴H为PA中点,
∴H为PA中点,
∴M为中线PB与中线EH的交点,
∴M是△APE的重心,∴![]() =
=![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到直线
到直线![]() 的距离相等.
的距离相等.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率为1的直线与曲线
且斜率为1的直线与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(l)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.
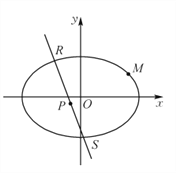
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个羽毛球协会的运动员人数分别为18,9,18,先采用分层抽样的方法从这三个协会中抽取5名运动员参加比赛.
(1)求应从这三个协会中分别抽取的运动员人数;
(2)将抽取的5名运动员进行编号,编号分别为![]() ,从这5名运动员中随机抽取2名参加双打比赛. 设“编号为
,从这5名运动员中随机抽取2名参加双打比赛. 设“编号为![]() 的两名运动员至少有一人被抽到” 为事件A,求事件A发生的概率.
的两名运动员至少有一人被抽到” 为事件A,求事件A发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com