
【题目】如图,正三棱柱ABC﹣A1B1C1的所有棱长都为2,D为CC1中点.试用空间向量知识解下列问题: 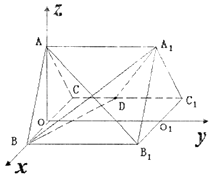
(1)求证:平面ABB1A1⊥平面A1BD;
(2)求二面角A﹣A1D﹣B的大小.
【答案】
(1)证明:取BC中点O,连AO,∵△ABC为正三角形,
∴AO⊥BC,
∵在正三棱柱ABC﹣A1B1C1中,
平面ABC⊥平面BCC1B1,
∴AD⊥平面BCC1B1,
取B1C1中点为O1,以O为原点,
![]() ,
, ![]() ,
, ![]() 的方向为x,y,z轴的正方向,
的方向为x,y,z轴的正方向,
建立空间直角坐标系,
则 ![]() .
.
∴ ![]() ,
,
∵ ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() ,∴AB1⊥面A1BD.…(5分)
,∴AB1⊥面A1BD.…(5分)
AA1面A1BD
所以 平面ABB1A1⊥面A1BD
(2)解:设平面A1AD的法向量为 ![]() ,
, ![]() .
.
![]() ,∴
,∴ 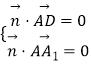 ,∴
,∴ ![]()
![]() ,
,
令z=1,得 ![]() 为平面A1AD的一个法向量,
为平面A1AD的一个法向量,
由(1)知AB1⊥面A1BD,
∴ ![]() 为平面A1AD的法向量,
为平面A1AD的法向量, 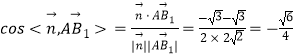 ,
,
∴二面角A﹣A1D﹣B的正弦值为 ![]() =
= ![]() .
.
【解析】(1)取BC中点O,连AO,利用正三角形三线合一,及面面垂直的性质可得AO⊥平面BCB1C1 , 取B1C1中点为O1 , 以O为原点, ![]() ,
, ![]() ,
, ![]() 的方向为x,y,z轴的正方向,建立空间直角坐标系,求出AB1的方向向量,利用向量垂直的充要条件及线面垂直的判定定理可得AB1⊥平面A1BD,即可证明平面ABB1A1⊥平面A1BD;(2)分别求出平面A1AD的法向量和平面A1AD的一个法向量代入向量夹角公式,可得二面角A﹣A1D﹣B的余弦值大小.
的方向为x,y,z轴的正方向,建立空间直角坐标系,求出AB1的方向向量,利用向量垂直的充要条件及线面垂直的判定定理可得AB1⊥平面A1BD,即可证明平面ABB1A1⊥平面A1BD;(2)分别求出平面A1AD的法向量和平面A1AD的一个法向量代入向量夹角公式,可得二面角A﹣A1D﹣B的余弦值大小.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)当a=﹣1时,求函数f(x)的最大值和最小值;
(2)当a∈R时,求函数f(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1= ![]() ,AB=1,AD=2,E为BC的中点,点M为棱AA1的中点.
,AB=1,AD=2,E为BC的中点,点M为棱AA1的中点. 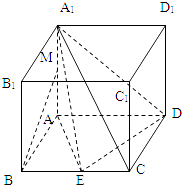
(1)证明:DE⊥平面A1AE;
(2)证明:BM∥平面A1ED.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①函数y=﹣ ![]() 在其定义域上是增函数;
在其定义域上是增函数;
②函数y= ![]() 是奇函数;
是奇函数;
③函数y=log2(x﹣1)的图象可由y=log2(x+1)的图象向右平移2个单位得到;
④若( ![]() )a=(
)a=( ![]() )b<1.则a<b<0
)b<1.则a<b<0
则下列正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a﹣c= ![]() b,sinB=
b,sinB= ![]() sinC.
sinC.
(1)求cosA的值;
(2)求cos(A+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数y=kx+1在R上是增函数,命题q:x∈R,x2+(2k﹣3)x+1=0,如果p∧q是假命题,p∨q是真命题,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com