练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知f（x）=
    x+π，(x＞0)
    0，      (x≤0)
    ，则f[f（-1）]=（　　）
    A、π-1B、0C、1D、π
    考点：函数的值
    专题：函数的性质及应用
    分析：利用分段函数的性质求解．
    解答： 解：∵函数f（x）=
    x+π，(x＞0)
    0，(x≤0)
    ，
    ∴f（-1）=0，
    f[f（-1）]=f（0）=0．
    故选：B．
    点评：本题考查函数值的求法，解题时要认真审题，注意分段函数的性质的灵活运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知等差数列{an}的前n项和为Sn，且a3=3，S4=10．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn=
    1
    anan+1
    ，求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在三角形ABC中，acosB=bcosA，则三角形ABC是（　　）
    A、钝角三角形
    B、直角三角形
    C、等腰三角形
    D、等边三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    反比例函数y=
    k
    x
    与一次函数y=x-
    3
    2
    在（-1，1）有交点，则k的取值范围为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列各组中两个函数是同一函数的是（　　）
    A、f(x)=
    x2-1
    x-1
    与g（x）=x+1
    B、f（r）=πr2（r≥0）与g（x）=πx2（x≥0）
    C、f(x)=logaax(a＞0，且a≠1）与g(x)=alogax(a＞0，且a≠1)
    D、f(x)=|x|与g(t)=(
    		t
    )2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    用反证法证明命题：“已知a、b为实数，若a＞0，b＜0，则方程x2+ax+b=0?至少有一个实根”时，要做的假设是（　　）
    A、方程x2+ax+b=0没有实根
    B、方程x2+ax+b=0至多有一个实根
    C、方程x2+ax+b=0至多有两个实根
    D、方程x2+ax+b=0恰好有两个实根

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点A（1，2），B（-3，8）．
    （1）求直线AB的方程；
    （2）若点P满足
    PA
    •
    PB
    =0，求P点的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A={x|-1≤x≤2}，B={x|x2-（2m+1）x+2m＜0}．
    （Ⅰ）当m＜
    1
    2
    时，化简集合B；
    （Ⅱ）若“x∈B”是“x∈A”的充分条件（A∪B=A），求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

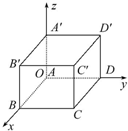    如图，已知长方体ABCD-A′B′C′D的边长为AB=12，AD=8，AA′=5．以这个长方体的顶点A为坐标原点，射线AB，AD，AA′分别为x轴、y轴、z轴的正半轴，建立空间直角坐标系，
    （1）求长方体顶点C′的坐标．
    （2）计算A、C′两点间的距离．

    查看答案和解析>>

    同步练习册答案