
【题目】已知![]() ,
,![]() .
.
(1)讨论![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 和
和![]() 上单调递增.(2)见解析
上单调递增.(2)见解析
【解析】
(1)先求函数的定义域,再进行求导得![]() ,对
,对![]() 分成
分成![]() ,
,![]() ,
,![]() 三种情况讨论,求得单调区间;
三种情况讨论,求得单调区间;
(2)要证由![]() ,等价于证明
,等价于证明![]() ,再对
,再对![]() 分
分![]() ,
,![]() 两种情况讨论;证明当
两种情况讨论;证明当![]() 时,不等式成立,可先利用放缩法将参数
时,不等式成立,可先利用放缩法将参数![]() 消去,转化成证明不等式
消去,转化成证明不等式![]() 成立,再利用构造函数
成立,再利用构造函数![]() ,利用导数证明其最小值大于0即可。
,利用导数证明其最小值大于0即可。
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ;
;
由![]() ,得
,得![]() ;
;
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ;
;
所以![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 和
和![]() 上单调递增.
上单调递增.
(2)由![]() ,得
,得![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,不等式显然成立;
,不等式显然成立;
②当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() ,
,
所以只需证:![]() ,
,
即证![]() ,令
,令![]() ,
,
则![]() ,
,![]() ,
,
令![]() ,
,
则![]() ,
,
令![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上为增函数,
上为增函数,
因为![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又因为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以![]() ,
,
所以原命题得证


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .
.
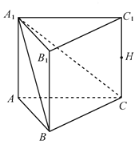
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:,
![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为其焦点,
为其焦点,![]() 为其准线,过
为其准线,过![]() 任作一条直线交抛物线于
任作一条直线交抛物线于![]() 两点,
两点,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 在
在![]() 上的射影,
上的射影,![]() 为
为![]() 的中点,给出下列命题:
的中点,给出下列命题:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() 与
与![]() 的交点的
的交点的![]() 轴上;(5)
轴上;(5)![]() 与
与![]() 交于原点.
交于原点.
其中真命题的序号为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在正常数
,若存在正常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立,我们称函数
成立,我们称函数![]() 为“
为“![]() 同比不减函数”.
同比不减函数”.
(1)求证:对任意正常数![]() ,
,![]() 都不是“
都不是“![]() 同比不减函数”;
同比不减函数”;
(2)若函数![]() 是“
是“![]() 同比不减函数”,求
同比不减函数”,求![]() 的取值范围;
的取值范围;
(3)是否存在正常数![]() ,使得函数
,使得函数![]() 为“
为“![]() 同比不减函数”,若存在,求
同比不减函数”,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为信号源点,
为信号源点,![]() 、
、![]() 、
、![]() 是三个居民区,已知
是三个居民区,已知![]() 、
、![]() 都在
都在![]() 的正东方向上,
的正东方向上,![]() ,
,![]() ,
,![]() 在
在![]() 的北偏西45°方向上,
的北偏西45°方向上,![]() ,现要经过点
,现要经过点![]() 铺设一条总光缆直线
铺设一条总光缆直线![]() (
(![]() 在直线
在直线![]() 的上方),并从
的上方),并从![]() 、
、![]() 、
、![]() 分别铺设三条最短分支光缆连接到总光缆
分别铺设三条最短分支光缆连接到总光缆![]() ,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/
,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/![]() ,设
,设![]() ,(
,(![]() ),铺设三条分支光缆的总费用为
),铺设三条分支光缆的总费用为![]() (元).
(元).
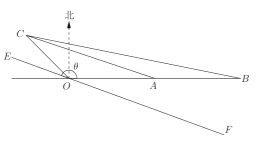
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
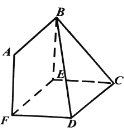
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为
为![]() 上一个动点,过点
上一个动点,过点![]() 与椭圆
与椭圆![]() 只有一个公共点的直线为
只有一个公共点的直线为![]() ,过点
,过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() ,求证:
,求证:![]() 与
与![]() 的交点在定直线上,并求出该定直线的方程.
的交点在定直线上,并求出该定直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com