
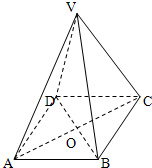
 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 的等腰三角形,AC∩BD=O.
的等腰三角形,AC∩BD=O.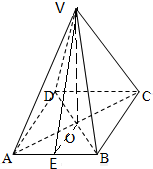
 ,O是底面正方形ABCD的中心,
,O是底面正方形ABCD的中心,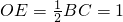 ,
,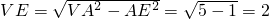
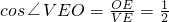 ,可得∠VEO=60°
,可得∠VEO=60° ×AB×VE=2,S△OAB=
×AB×VE=2,S△OAB= ×AB×EO=1,VO=
×AB×EO=1,VO= =
=
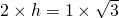 ,得
,得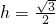
 .
.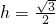 ,即得点O到平面VAB的距离的大小.
,即得点O到平面VAB的距离的大小.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
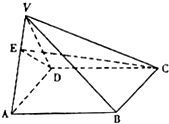 (2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD三角形,平面VAD⊥底面ABCD,设AB=2
(2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD三角形,平面VAD⊥底面ABCD,设AB=2查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ASCD.设AB=2.
(2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ASCD.设AB=2.查看答案和解析>>
科目:高中数学 来源:2012年河南省新乡、许昌、平顶山高考数学一模试卷(理科)(解析版) 题型:解答题
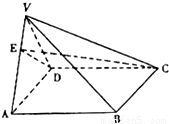
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com