分析:(1)以D为原点,DA,DC,DD1,分别为X,Y,Z轴,分别求出各点的坐标,进而求出直线AF的方向向量及平面BDE的法向量,代入线面夹角向量法公式,即可得到满足条件的E的坐标,进而求出答案.
(2)求出平面A1BE的一个法向量的坐标及平面BDE的一个法向量的坐标,代入二面角向量法公式,即可得到二面角A1-BE-D的余弦值.
解答: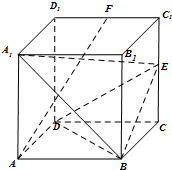
解:(1)建立如图所示空间直角坐标系,
D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0)F(0,1,2),A
1(2,0,2),B
1(2,2,2),C
1(0,2,2)(2分)
(1)设CE=a,则E(0,2,a)
设
=(x,y,z)是平面BDE的一个法向量,
,
=(a,-a,2),(4分)
又
=(-2,1,2),又
•=0,
CE=a=(6分)
(2)设
=(x,y,z)是平面A
1BE的法向量
,
=(1,2,2),(8分)
又
=(1,-1,2),
cos<,>=,(11分)
所以二面角A
1-BE-D的余弦值为
(12分)
点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面平行的性质,其中建立空间坐标系,然后将空间直线与平面、平面与平面位置关系转化为向量之间的关系,是解答本题的关键.

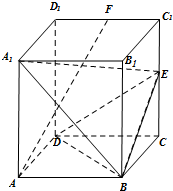 如图,四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1⊥底面ABCD,
如图,四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1⊥底面ABCD, 解:(1)建立如图所示空间直角坐标系,
解:(1)建立如图所示空间直角坐标系,

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案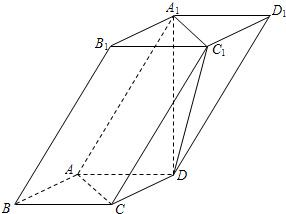 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.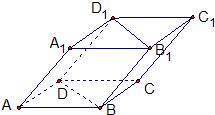 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是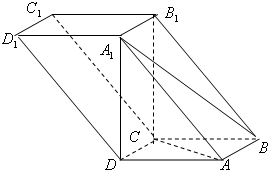 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2, (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD. (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,