
【题目】如图,已知![]() 是棱长为3的正方体,点
是棱长为3的正方体,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,(1)求证:
,(1)求证: ![]() 四点共面; (2)若点
四点共面; (2)若点![]() 在
在![]() 上,
上, ![]() ,点
,点![]() 在
在![]() 上,
上, ![]() ,垂足为
,垂足为![]() ,求证:
,求证: ![]() 面
面![]() ; (3)用
; (3)用![]() 表示截面
表示截面![]() 和面
和面![]() 所成锐二面角大小,求
所成锐二面角大小,求![]() .
.

【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)四点共面问题通常我们将它们变成两条直线,然后证明这两条直线平行或相交,根据公理3的推论2、3可知,它们共面;(2)要证线面垂直,可以证明两个垂直平面内一条直线垂直两平面的交线即可;(3)可以证明![]() 就是二面角的平面角,在直角三角形中可解得
就是二面角的平面角,在直角三角形中可解得![]() 的值.
的值.
试题解析:(1)证明:在DD![]() 上取一点N使得DN=1,连接CN,EN,显然四边形CFD
上取一点N使得DN=1,连接CN,EN,显然四边形CFD![]() N是平行四边形,所以D
N是平行四边形,所以D![]() F//CN,同理四边形DNEA是平行四边形,所以EN//AD,且EN=AD,又BC//AD,且AD=BC,所以EN//BC,EN=BC,所以四边形CNEB是平行四边形,所以
F//CN,同理四边形DNEA是平行四边形,所以EN//AD,且EN=AD,又BC//AD,且AD=BC,所以EN//BC,EN=BC,所以四边形CNEB是平行四边形,所以
CN//BE,所以D![]() F//BE,所以
F//BE,所以![]() 四点共面。
四点共面。
(2)因为![]() 所以
所以![]() ∽
∽![]() MBG,所以
MBG,所以![]() ,即
,即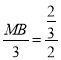 ,所以MB=1,因为AE=1,所以四边形ABME是矩形,所以EM⊥BB
,所以MB=1,因为AE=1,所以四边形ABME是矩形,所以EM⊥BB![]() 又平面ABB
又平面ABB![]() A
A![]() ⊥平面BCC
⊥平面BCC![]() B
B![]()
,且EM在平面ABB![]() A
A![]() 内,所以
内,所以![]() 面
面![]()
(3)![]() 面
面![]() ,所以
,所以![]() BF,
BF, ![]() MH,
MH, ![]() ,所以∠MHE就是截面
,所以∠MHE就是截面![]() 和面
和面![]() 所成锐二面角的平面角,∠EMH=
所成锐二面角的平面角,∠EMH=![]() ,所以
,所以![]() ,ME=AB=3,
,ME=AB=3, ![]() ∽
∽![]() MHB,所以3:MH=BF:1,BF=
MHB,所以3:MH=BF:1,BF=![]() ,所以MH=
,所以MH=![]() ,所以
,所以![]() =
=![]()


科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 上顶点为
上顶点为![]() ,右顶点为
,右顶点为![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 过点
过点![]() ,直线
,直线![]() 与圆
与圆![]() 相交得到的弦长为
相交得到的弦长为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点, ![]() 与
与![]() 轴,
轴, ![]() 轴分别相交于
轴分别相交于![]() 两点,满足:①记
两点,满足:①记![]() 的中点为
的中点为![]() ,且
,且![]() 两点到直线
两点到直线![]() 的距离相等;②记
的距离相等;②记![]() 的面积分别为
的面积分别为![]() 若
若![]() 当
当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最小正周期是
)的最小正周期是 ![]() ,最小值是﹣2,且图象经过点(
,最小值是﹣2,且图象经过点( ![]() ,0),则f(0)= .
,0),则f(0)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数k的值;
,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x2+mx+1=0有两个不等的负根;命题q:4x2+4(m﹣2)x+1=0无实根.若命题p与命题q有且只有一个为真,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x不等式x2﹣2mx+m+2<0(m∈R)的解集为M.
(1)当M为空集时,求m的取值范围;
(2)在(1)的条件下,求![]() 的最大值;
的最大值;
(3)当M不为空集,且M![]() [1,4]时,求实数m的取值范围.
[1,4]时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为了测量正在海面匀速行驶的某船的速度,在海岸上选取距离1千米的两个观察
点C、D,在某天10:00观察到该船在A处,此时测得∠ADC=30°,2分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,
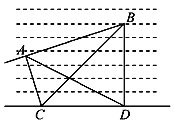
求该船航行的速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD= ![]() AA1=2.
AA1=2. 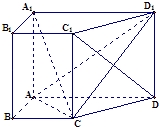
(1)求证:直线C1D⊥平面ACD1;
(2)试求三棱锥A1﹣ACD1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com