
| A. | 等差数列,公差为eax | B. | 等差数列,公差为-eax | ||
| C. | 等比数列,公比为eax | D. | 等比数列,公比为-eax |
分析 求出导数,运用两角和的正弦公式化简,求出导数为0的根,讨论根附近的导数的符号相反,即可得到极值点,求得极值,运用等比数列的定义即可得证;
解答 解::f′(x)=eax(asinx+cosx)=$\sqrt{{a}^{2}+1}$•eaxsin(x+φ),
tanφ=$\frac{1}{a}$,0<φ<$\frac{π}{2}$,
令f′(x)=0,由x≥0,x+φ=mπ,即x=mπ-φ,m∈N*,
对k∈N,若(2k+1)π<x+φ<(2k+2)π,即(2k+1)π-φ<x<(2k+2)π-φ,
则f′(x)<0,因此在((m-1)π-φ,mπ-φ)和(mπ-φ,(m+1)π-φ)上f′(x)符号总相反.
于是当x=nπ-φ,n∈N*,f(x)取得极值,所以xn=nπ-φ,n∈N*,
此时f(xn)=ea(nπ-φ)sin(nπ-φ)=(-1)n+1ea(nπ-φ)sinφ,
易知f(xn)≠0,而$\frac{{f(x}_{n+1})}{{f(x}_{n})}$=$\frac{{(-1)}^{n+2}{e}^{a((n+1)π-φ)}sinφ}{{(-1)}^{n+1}{e}^{a(nπ-φ)}sinφ}$=-eaπ是常数,
故数列{f(xn)}是首项为f(x1)=ea(π-φ)sinφ,公比为-eaπ的等比数列;
故选:D.
点评 本题考查导数的运用:求极值和单调区间,主要考查三角函数的导数和求值,同时考查等比数列的定义和通项公式的运用,考查不等式恒成立问题的证明,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
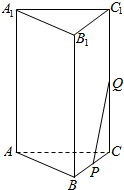 如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.
如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com